© 2010 Rasmus ehf og Jóhann Ísak
Funksjoner 2
|
© 2010 Rasmus ehf og Jóhann Ísak |
Funksjoner 2 |
|
Funksjoner kan kombineres på mange forskjellige måter. Vi skal se på noen av dem.
Gitt funksjonene f(x) = x2 + x og g(x) = x + 1.
a) Finn summen av f og g.
f(x) + g(x) = (x2 + x) + (x + 1) = x2 + 2x + 1
b) Finn differensen mellom f og g.
f(x) – g(x) = (x2 + x) – (x + 1) = x2 + x –x – 1 = x2 – 1
c) Finn 2f(x) – 3g(x).
2f(x) – 3g(x) = 2(x2 + x) – 3(x + 1) = 2x2 + 2x – 3x – 3
= 2x2 – x – 3
d) Multipliser f og g.
f(x)·g(x) = (x2 + x)·(x + 1) = x3 + x2 + x2 + x = x3 + 2x2 + x
e) Del f på g.
Løsningen på del e) er en rett linje der y = x. Legg merke til at funksjonen f(x)/g(x) = x ikke er definert for x = –1, fordi man ikke kan dele noe på null. Hvis både f og g er definert for alle reelle tall, mengden R, er f(x)/g(x) = Df/g = R\{–1}. Grafen til(x)/g(x) vil derfor være en rett linje y = x med et hull i x = –1.
En funksjon kan virke på resultatet av en annen funksjon. Vi kan for
eksempel kombinere funksjonene f og g,
og skrive f(g(x)) (uttales f av g av x).
Dette kalles en sammensatt funksjon.
Gitt funksjonene f(x) = x2 + x og g(x) = x + 1.
a) Finn f(g(x)).
f(g(x)) = f(x + 1) = (x + 1)2 + (x + 1) = x2 + 2x + 1 + x + 1 = x2 + 3x + 2
b) Finn g(f(x)).
g(f(x)) = g(x2 + x) = x2 + x + 1
c) Finn f(f(x)).
f(f(x)) = f(x2 + x) = (x2 + x)2 + (x2 + x) = x4 + 2x3 + 2x2 + x
d) Finn g(g(x)).
g(g(x)) = g(x + 1) = (x + 1) + 1 = x + 2
I den sammensatte funksjonen f(g(x)), kaller vi g(x) den indre funksjonen, og f(x) den ytre funksjonen. Den indre funksjonen fungerer som en variabel i den ytre funksjonen.
Gitt funksjonene f(x)
= 
og g(x)
= x2 + 1.
a) Finn f(g(x)).
f(g(x)) = f(x2 + 1)
=
b) Finn g(f(x)).
g(f(x)) =
g()=
= x + 1
Vi har allerede lært om translasjon av funksjoner. Vi kan se på translasjoner som sammensatte funksjoner. Se på det neste eksempelet.
Vi skal translatere grafen til funksjonen
f(x) = x3 – x
med vektoren 
.Den følgende verditabellen gjelder for x - verdier mellom –2
og 2.
Først regner vi ut
f(x).
Deretter flytter vi alle
resultatene ned en enhet (x = - 1 blir for eksempel x = -2). Dette blir det
samme som å regne ut f(x–1). Til slutt legger vi til 3
til alle resultatene.
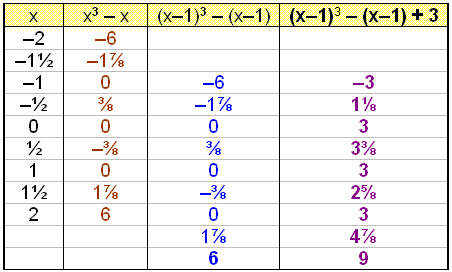
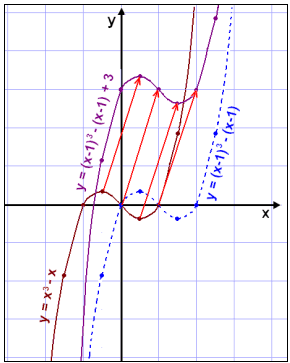
Vi ser av tegningen at når
vi translaterer grafen til f(x) en enhet til høyre, får vi
grafen til f(x–1) (se den blå grafen). Når vi
legger 3 til den blå grafen, flyttes den opp tre enheter. Hvert punkt på den
opprinnelige grafen f(x) har blitt translatert med vektoren
.
Vi vet derfor denne regelen gjelder:
|
Når vi translaterer grafen
f(x) med vektoren
får vi grafen f(x–a) + b. |
Vi skal nå se på funksjonene f(x) = 
og g(x) = 4 – x2,
og finne definisjonsmengden og verdiområdet til de sammensatte funksjonene.
Vi må selvfølgelig begrense verdiene under
rottegnet til kun ikke - negative tall. Den sammensatte funksjonen f(g(x)) = 
kan derfor bare inneholde positive verdier
av g(x) = 4 – x2
.
Dette betyr at vi må begrense definisjonsmengden
til den indre funksjonen g(x) slik at den bare gir ikke - negative tall. Tenk på
dette mens du ser på grafen til g(x) = 4
– x2. Verditabellen blir slik:
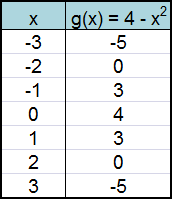
Grafen ser slik ut:
.
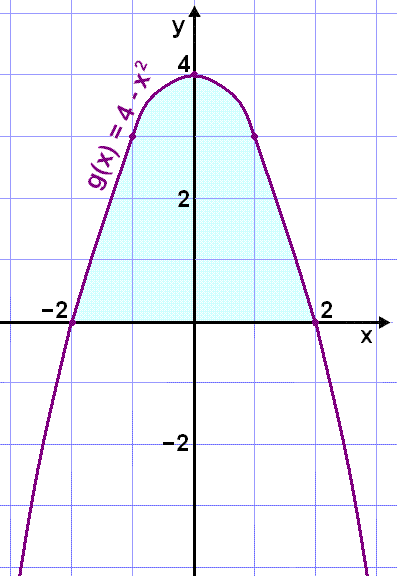
Den skraverte delen av grafen viser hvor g(x) ligger over x - aksen. I intervallet mellom - 2 og 2, har den indre funksjonen g(x) ikke - negative verdier fra 0 til 4.
Hvis vi velger definisjonsmengden
g(x)
eller Dg(x) =
{x
R |
–2 
x
2},
får vi verdiområdet Rg(x) =
{y
R | 0
y
4}.
Dette
må være definisjonsmengden til f(x) i den sammensatte funksjonen. Hvis vi velger
verdier for x i intervallet 0
x
4,
får f(x)
verdier mellom
0
x
2.
Vi har vist at definisjonsmengden til
f(g(x))
er Df(g(x)) =
{x
R |
–2
x
2}
og verdiområdet til f(g(x))
er Rf(g(x)) =
{ y R | 0
x
2 }. Se
til slutt på grafen.
Først verditabellen.
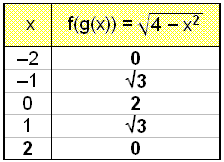
Grafen er en halvsirkel med sentrum i (0, 0) og radius 2.
 |
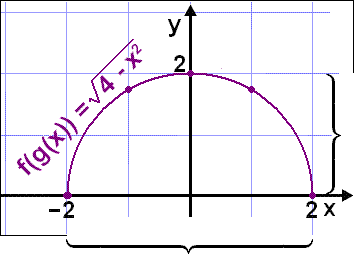Rf(g(x)) =
{ y
|
Df(g(x)) =
{x
R |
–2
x
2
Her er en fremgangsmåte for å finne definisjonsmengden og verdiområdet til en sammensatt funksjon:
|
1) Velg definisjonsmengde for den indre funksjonen, slik at verdiområdet kan brukes som definisjonsmengde for den ytre funksjonen. 2) Når du har funnet definisjonsmengden til den ytre funksjonen, kan du også finne verdiområdet. |
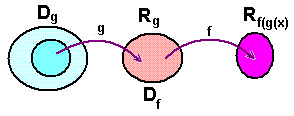
Noen ganger, som i eksempelet over, kan bare en del av definisjonsmengden g brukes. Verdiområdet blir definisjonsmengden til den ytre funksjonen f. Verdien av f blir verdiområdet til den sammensatte funksjonen f(g(x)).
Se på eksemplene, og regn deg gjennom test 1 i Funksjoner 2.
Husk å fylle ut sjekklisten underveis.
