© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Faktorisering av polynomer

Introduksjon 1

Divisjon av polynomer og rest-teoremen.

Se på funksjonen f(x) = 6x2 − 9x + 3, velg noen x-verdier og lag en verditabell. Tenkt deg at vi har hatt flaks. Vi valgte x = 1, og så at f(1) = 0.

Hvis x = 1, vil det si at (x − 1) = 0.

At f(1) = 0 forteller oss at (x − 1) er en faktor av f(x).

Hvis vi regner med at (x−1) er en faktor av f(x) kan vi også vise at
f(1) = 0:

f(x) = 6x2 − 9x + 3 = (ukjent faktor)(x − 1)

  f(1) = 6 − 9 + 3 = (ukjent faktor)(1 − 1) = (ukjent faktor)∙0

         = 0

Til slutt må vi dividere 6x2 − 9x + 3 med x − 1 for å finne den ukjente faktoren.

Vi skal nå lære å gjøre dette ved å sammenligne polynom-divisjon med vanlig tall-divisjon.

Eksempel 1

Tall-divisjon: 

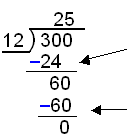Hvor mange ganger går 12 opp i 30? Svaret er 2. Nå ganger du 2x12=24. Trekk 24 fra 30 og flytt 0 ned.

Hvor mange ganger går 12 opp i 60?
5 ganger. 5x12 = 60.
Trekk 60 fra 60.

Polynom-divisjon:

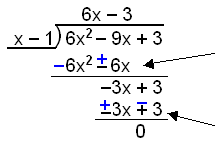Hvor mange ganger går x – 1 opp i 6x2? Vi trenger bare å finne ut hvor mange ganger x går opp i 6x2, eller hva vi må gange x med for å få 6x2. Svaret er 6x. Nå ganger vi 6x∙(x − 1) = 6x2 − 6x.

Trekk fra 6x2 − 6x ved å endre fortegnene foran hvert ledd.
 Deretter flytter vi ned 3. Så finner vi ut hvor mange ganger x – 1 går opp i -3x, eller hva vi må gange x med for å få -3x. −3×(x − 1) = −3x + 3. Trekk fra −3x + 3 ved å endre fortegnene. Resten er 0.

f(x) = 6x2 − 9x + 3 kan faktoriseres fullt ut:

f(x) = (6x − 3)(x − 1) = 3(2x−1)(x − 1).

Eksempel 2

Vi kan også faktorisere 6x2 − 9x + 3 ved hjelp av formelen for annengradslikninger. 

Koeffisientene er a = 6, b = −9 and c = 3.

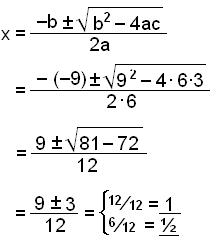
Løsningene på likningen er x = 1 og x = ½, så parentesene (x − 1) og (x − ½) må begge være faktorer av 6x2 − 9x + 3. Ferdig faktorisert blir likningen slik:

    6x2 − 9x + 3 = 6(x − 1)(x − ½).

Vi må gange med seks for å få riktig svar når vi ganger sammen faktorene.

Dette eksempelet gir oss regelen for faktorisering av annengradslikninger til to brøker.

ax2 + bx + c = a(x − r1)(x − r2)

Verdiene r1 og r2 kalles RØTTENE til funksjonen. Disse finner vi ved å løse annengradslikningen. 

Eksempel 3

Vi skal nå dividere x3 − 6x2 + 11x − 6 på x − 1 og bruke resultatet til å faktorisere polynomet.

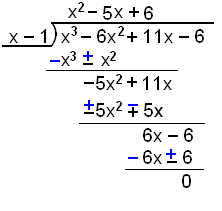X3 delt på x er x2.

x2(x − 1) = x3 − x2. Trekk fra x3 − x2 Ved å endre fortegnene.

Flytt 11x ned. x går opp −5x ganger i −5x2. −5x(x − 1) = −5x2 + 5x.

Trekk fra −5x2 + 5x ved å endre fortegn. Flytt −6 ned. X går 6 ganger opp i 6x. 6(x − 1) = 6x − 6. Trekk fra.

Resten er 0, og (x−1) er altså en faktor i polynomet. Vi kan faktorisere annengradslikningen på en av måtene som vi har brukt tidligere.

x3 − 6x2 + 11x − 6 = (x2 − 5x + 6)(x − 1) = (x − 3)(x − 2)(x − 1)

Eksempel 4

Nå skal vi se på et vanskeligere eksempel.

Divider polynomet x3 − 4x + 3 med x − 1 og faktoriser

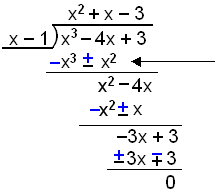Her kan vi ikke trekke fra x2 og −4x,

Så begge leddene blir stående uforandret.

 

Resten er 0, så x − 1 må være en faktor. Nå har vi igjen å faktorisere x2 + x − 3. Vi kan ikke få det til ved å prøve og feile, så vi må bruke formelen.

  Koeffisientene er a = 1, b = 1 og c = −3.

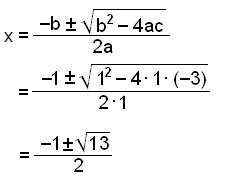
Ferdig faktorisert blir polynomet slik:

x3 − 4x + 3 = (x2 + x − 3)(x − 1)

Eksempel 5

Nå skal vi se på hva som skjer når resten ikke er 0.

Del x3 + 4x2 + x + 1 på x + 1.

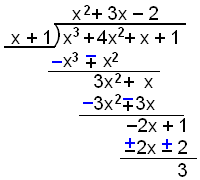
Her er resten 3.

Vi kan omskrive polynomet som:

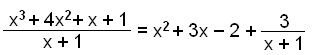
Denne skrivemåten er viktig for å få til det som kommer nå:

Fra dette eksemplet kan vi se det generelle resultatet:

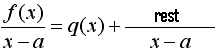
Hvor f(x) er et polynom som deles på (x-a) og q(x) er resultatet.

Hvis vi ganger begge sider av likningen med x – a får vi

    f(x) = q(x)(x − a) + rest

Nå skal vi bruke denne versjonen av f(x) til å regne ut f(a).

    f(a) = q(a)(a − a) + rest

    f(a) = q(x)∙0 + rest

    f(a) = rest

Dette viser oss at vi kan finne resten når et polynom deles på x-a uten å utføre divisjonen.

Dette kalles rest-teoremen og uttrykkes slik:

  Hvis polynomet f(x) deles på x − a blir resten f(a).

Eksempel 6

Bruk rest-teoremen til å finne resten når x3 + 4x2 + x + 1 deles x + 1.

Hvis vi kan omskrive x + 1 som x−(−1), kan vi bruke rest-teoremen på a = −1.

    f(−1) = (−1)3 + 4∙(−1)2 + (−1) + 1

            = −1 + 4 − 1 + 1

            = 3

Hvis du ser på forrige eksempel, ser du at det ble samme svar som her.

Eksempel 7

Til slutt bruker vi rest-teoremen til å finne resten når x3 + 4x2 + x + 1 deles på x − 1 ved å regne ut f(1).

    f(1) = 13 + 4∙12 + 1 + 1

          = 1 + 4 + 1 + 1

          = 7

Prøv Test 1 i Faktorisering av polynomer.

Husk å bruke sjekklisten.