Trigonometriske formler

Introduksjon 1

Enhetsformelen

Vi har mange formler og regler som skal gjøre det lettere å løse trigonometriske likninger.

Nå skal vi komme frem til, og lære å bruke, en av de mest nyttige formlene, Enhetsformelen.

Tegningen viser en rettvinklet trekant tegnet inn i enhetssirkelen. Enhetsformelen gjelder for alle punkter P på enhetssirkelen.

Det vil si at

(sin v)²+(cosv)²=1.

Vi skriver det vanligvis på formen:

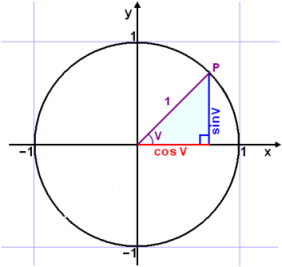sin²v + cos²v = 1

Og kan omskrive det slik:

sin²v = 1 − cos²v

Og slik:

cos²v = 1 - sin²v

Eksempel 1

Finn sin x når cos x = ⅓ og 0 x < /₂ (x er en vinkel mellom 0° og 90°).

Vi kan løse oppgaven med en kalkulator, cos⁻¹(⅓) ≈ 70,53° og sin 70,53° ≈ 0,94. Hvis vi vil ha et eksakt svar, må vi bruke enhetsformelen.

Eksempel 2

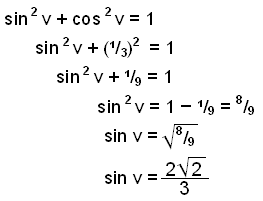
Bruk formelen sin²v + cos²v = 1 til å finne andre måter å skrive uttrykket ¹/ cos²v.

En måte er å flytte sin²v til den andre siden av likhetstegnet, så vi får cos²v = 1 − sin²v, deretter opphøye begge sider i -1. Da får vi

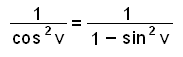
Vi kan også komme frem til uttrykket på en annen måte. Denne metoden kan ofte være veldig nyttig. Se hva som skjer hvis vi deler den opprinnelige likningen, sin²v + cos²v = 1, på cos²v.

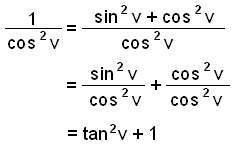
Vi har nå bevist formelen:

Eksempel 3

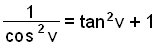
Nå skal vi bruke enhetsformelen til å finne verdien av sin²v og cos²v, gitt at sin²v = cos²v.

Først erstatter vi cos²v etter formelen cos²v = 1 − sin²v.

sin²v = cos²v

sin²v = 1 − sin²v

2∙sin²v = 1

sin²v = ½

Så erstatter vi sin²v etter formelen sin²v = 1 − cos²v.

sin²v = cos²v

1 − cos²v = cos²v

1 = 2∙cos²v

cos²v = ½

Eksempel 4

Løs likningen cos²x = sin x + 1

Sett først inn for cos²x.

cos²x = sin x + 1

1 − sin²x = sin x + 1

0 = sin²x + sin x = sin x (sin x + 1)

Dette gir oss at sin x = 0 or sin x = −1, slik at

Þá er x = k∙ (k∙180°) eða x = ³/₂ + k∙2 (270° + k∙360°).

Eksempel 5

Forenkle likningen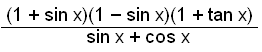

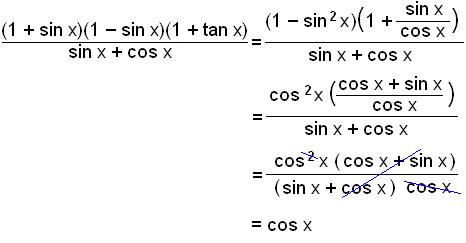Her bruker vi formelen

(a + b)(a − b) = a² − b² og skriver om tan x til ^{sin x}/_{cos x} før vi forenkler.

Prøv test 1 i Trigonometri.

Husk å bruke sjekklisten.