© 2008  Rasmus ehf    og Jóhann Ísak

Trigonometriske formler

Introduksjon 3  

Likninger av typen a sin x + b cos x = c

Figuren viser grafen til f(x) = sin x + 2 cos x.

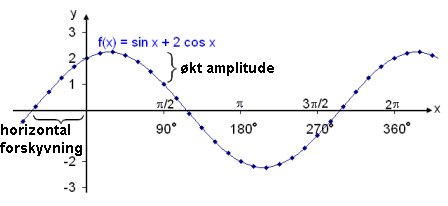
Utrolig nok ser dette ut som en vanlig sinusfunksjon, som har blitt forskjøvet og fått en økt amplitude. Vi har tidligere sett på hva som påvirker amplituden, og hvordan amplituden kan økes fra 1 ved å gange med en konstant større enn 1. (se trigonometriske funksjoner introduksjon 3). Vi har også sett at grafene til funksjonen kan forskyves til siden ved å legge en konstant til vinkelen. Ved hjelp av dette kan vi skrive om likningen på formen sin (x + v), slik at

   m sin (x + v) = sin x + 2 cos x

Nå ser vi på grafen  g(x) = sin x − 2 cos x.

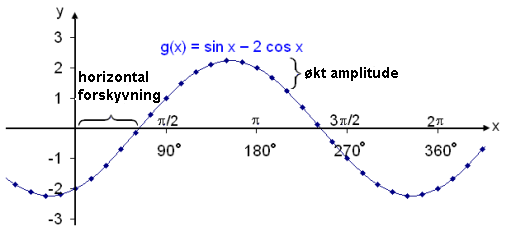
Dette er samme kurve som før, bortsett fra at forskyvningen er i motsatt retning. Vi setter opp denne likningen:

   m sin (x − v) = sin x − 2 cos x

Vi kan skrive om uttrykkene ved hjelp av enhetsformelen:

   sin (x + v) = sin x cos v + cos x sin v

   sin (x − v) = sin x cos v − cos x sin v

Vi ganger alle ledd med m:

   m sin (x + v) = m sin x cos v + m cos x sin v

   m sin (x − v) = m sin x cos v − m cos x sin v

Sammenlign resultatet med den opprinnelige likningen.

   m sin (x + v) =      1 sin x       + 2 cos x

                        = m cos v sin x + m sin v cos x

   m sin (x − v) =      1 sin x         − 2 cos x

                        = m cos v sin x  − m sin v cos x

Vi ser at dette gjelder i begge tilfeller:

   m cos v = 1

    m sin v = 2

Hvis vi deler den andre likningen på den første, får vi

   tan v = ²/₁

Dette gir vinkelen  v = tan⁻¹ (2) ≈ 63,4°.

Hvis vi tegner en rettvinklet trekant med sidene 1 og 2, samme verdier som i likningen, kan vi regne ut hypotenusen. Vi ser at:

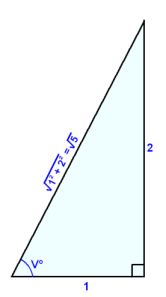
   cos v = 1/ og sin v = 2/.

Vi bruker likningene:

   m cos v = 1

    m sin v = 2.

Og ser at:

   m∙1/ = 1

           m =

Med andre ord kan vi skrive om likningen som:

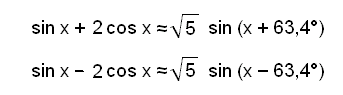
Vi ser at amplituden i funksjonene f(x) = sin x + 2 cos x og g(x) = sin x − 2 cos x er .

Vi bruker a og b som konstanter, og får de generelle formlene:

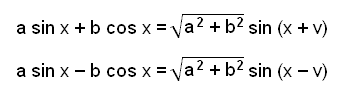Vinkel v kan vi finne slik:

Eksempel 1

Finn amplituden til funksjonen  f(x) = 3 sin x + 4 cos x.

Vi begynner med å skrive om funksjonen.

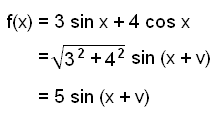
Amplituden er  5.

Eksempel 2

Grafen til funksjonen f(x) = 3 sin x + 4 cos x er en forskjøvet sinusfunksjon.

Regn ut hvor mange grader, og i hvilken retning den har blitt forskjøvet.

   f(x) = 3 sin x + 4 cos x

         = 5 sin (x + v)

      v = tan ⁻¹ (4/3) ≈ 53,1°

Bølgen har blitt forskjøvet 53.1° til venstre (f(x) ≈ 5 sin (x + 53,1°).

Eksempel 3

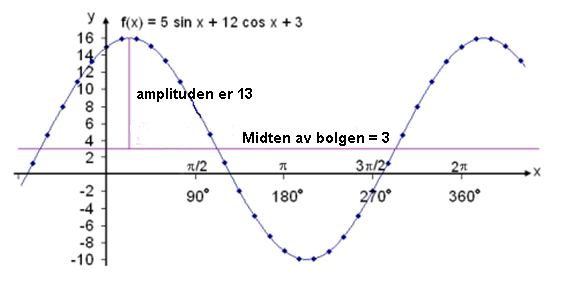
Gitt funksjonen f(x) = 5 sin x + 12 cos x + 3. Finn amplituden, bølgetoppen og forskyvingen.

Skriv om f(x).

   tan ⁻¹ (12/5) ≈ 67,4°

   f(x) = 13 sin (x + 67,4°) + 3

Amplituden er 13, så bølgetoppen er 13 + 3 = 16. Se på grafen.

Eksempel 4

Løs likningen  3 sin x + 4 cos x = 5 , 0° x < 360°.

   3 sin x + 4 cos x = 5

                              = 5 sin (x + 53,1°)

      sin (x + 53,1°) = 5/5 = 1

              x + 53,1° = sin ⁻¹ 1 = 90° + k∙360°

                            x = −53,1° + 90° + k∙360°

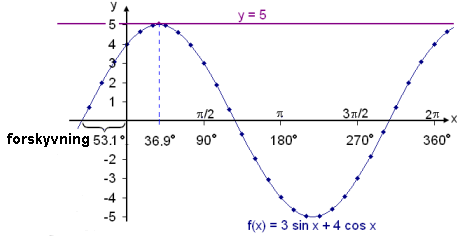
                            x = 36,9°

Vi får en løsning, 36,9° i første kvadrant.

Når vi ser på grafen, finner vi ingen andre løsninger i dette intervallet.

Eksempel 5

Finn alle løsninger på likningen sin x − cos x = 1.

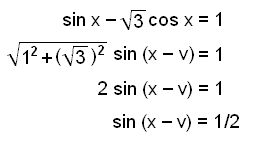
Vi ser at tan v = og v = tan () ⁻¹ = /₃ (60°).

   sin (x − /₃) = ½

                    x = /₃ + /₆ + k∙2

                       = /₂ + k∙2

En annen mulighet:

         (x − /₃) = − /₆ + k∙2

                     x = /₃ + −/₆ + k∙2

Prøv Test 3 i Trigonometriske formler.

Husk å bruke sjekklisten.