© 2010  Rasmus ehf    og Jóhann Ísak

Vektorer

Introduksjon 6  

Parameterform og polarkoordinater

Vi har allerede lært oss å regne ut koordinatene til et punkt ved hjelp av vektoren fra origo til punktet, og vektoraddisjon (se Introduksjon 3). Når vi kjenner vektorens retning, kan vi kontrollere lengden ved å multiplisere med et tall t.

Vi kan finne likningen til en linje hvis vi kjenner til et punkt P₁ = (x₁,y₁) på linjen og linjens retningsvektor.
.

Hvis P er et punkt på linjen, blir likningen

= + t·

og med koordinater

Vi kaller dette linjens parameterform, som generelt skrives som et lineært likningssystem der vi har en likning for x - koordinaten og en likning for y - koordinaten.

Bokstaven t kalles en parameter. For ulike verdier av t, får vi ulike punkter på linjen.

Eksempel 1

Vi skal skrive linjen y = 3x + 2 på parameterform.

Linjens normalform er 3x – y + 2 = 0, så normalvektoren er og retningsvektoren er

Vi velger x = 1 og får at y = 3·1 + 2 = 5. Det betyr at punktet (1, 5) er på linjen. Linjen på parameterform kan derfor skrives slik:

x = 1 + t y = 5 + 3t

Hvis vi velger t = 1, får vi at x = 1 + 1·1 = 2 og y = 5 + 3·1 = 8. Dette gir oss et annet punkt på linjen, nemlig (2, 8).

Hvis vi velger t = 2, får vi x = 1 + 1·2 = 3 og y = 5 + 3·2 = 11. Dette gir oss punktet (3, 11).

Hvis vi velger x = 4 og vil regne ut y, må vi først finne ut hvilken verdi av t som gir oss x = 4. Deretter bruker vi dette til å finne y - koordinaten.

   x = 1 + t = 4

               t = 4 – 1 = 3

   y = 5 + 3·3 = 14

Eksempel 2

Nå skal vi finne den opprinnelige likningen for en linje på parameterform.

x = 1 + t      som gir t = x – 1 y = 5 + 3t    som gir t = (y – 5)/3

Likningene over må ha samme verdi for t. Vi kan derfor sette den høyre siden av likningene lik hverandre:

    x – 1 = ^{(y – 5)}/3

  3x – 3 = y – 5

  3x + 2 = y

Dette er samme likning som vi begynte med i Eksempel 1.

Eksempel 3

Vi skal kontrollere om punktet(100, 302) ligger på linjen

x = 1 + t      y = 5 + 3t

Vi regner ut t.

100 = 1 + t  som gir t = 99 302 = 5 + 3t  som gir t = (302 – 5)/3 = 297/3 = 99

Likningene gir samme verdi for t. Punktet (100, 302) ligger på linjen.

Eksempel 4

Regn ut skjæringspunktet mellom to linjer på parameterform:

x = 1 + 2t y = 1 + t

og

x = 6 + 3r y = 1 – r

Vi bruker forskjellige bokstaver som parametre for linjene, fordi de er uavhengige av hverandre. I skjæringspunktet er derimot både x - koordinatene og y - koordinatene de samme. Vi kan derfor sette opp et likningssystem og løse det:

   x = 1 + 2t = 6 + 3r

og

   y = 1 + t = 1 – r

Dette gir oss likningssystemet

2t – 3r = 5 t  = –r

Nå kan vi sette inn –r istedenfor t i den øverste likningen.

   2(–r) – 3r = 5

             –5r = 5

                 r = –1 . Da blir t = 1

Vi regner ut x og y ved å sette inn verdier parameterne.

x = 1 + 2t = 1 + 2·1 = 3 y = 1 + t = 1 + 1 = 2

Vi kontrollerer svaret ved å gjøre det samme med den andre linjen.

x = 6 + 3r = 6 + 3(–1) = 3   y = 1 – r = 1 – (–1) = 2

Skjæringspunktet er (3, 2).

Parameterformen er veldig fleksibel, og tilbyr mer enn bare et likningssystem for rette linjer. I mange tilfeller er det til og med lettere å beskrive sammenhengen mellom x og y i parameterform enn i en vanlig likning. Parameterformen gir oss egne likninger for x og y, med parameteren t som styrer forandringene i koordinatene. Likningssystemet på generell form:

x = f(t) y = g(t)

For å skrive om likningssystemet på parameterform, til en likning med x og y, må vi løse likningene i likningssystemet med hensyn på t.

Eksempel 5

Skriv om likningen på parameterform, til en vanlig likning med x og y:

x = t + 1 y = t2 – 1

Fra den øverste likningen finner vi at t = x – 1 og t² = x² – 2x + 1

Fra den nederste likningen får vi t² = y + 1. Dette gir oss at

   y + 1 = x² – 2x + 1

         y = x² – 2x

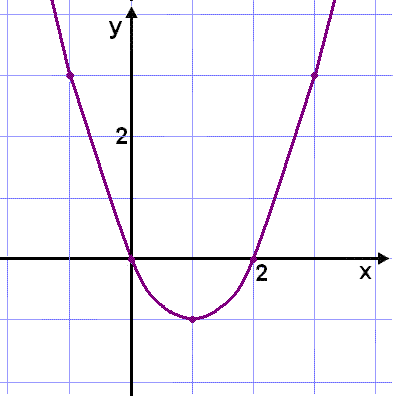
Dette er en parabel med nullpunkter i x = 0 og x = 2.

Vi bruker likningen på parameterform til å tegne opp kurven.
Vi lar t gå fra -2 til 2, og regner ut x og y.

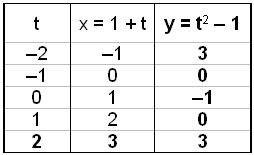Vi ser at det går minst like bra å regne ut verdiene i en tabell når likningen er på parameterform, som ellers.

Vi kan også tegne opp kurven på en grafisk kalkulator som CASIO, selv om likningen er på parameterform. Først må vi gjøre noen innstillinger.

Vi begynner med å velge GRAPH, og deretter V-Window med

Vi får opp denne menyen:

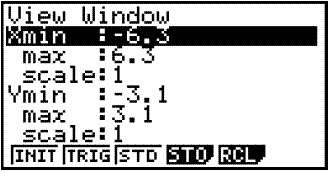
Vi trykker på pilen ned fem ganger, til den nederste linjen er markert. Trykk en gang til på pil ned for å åpne neste meny.

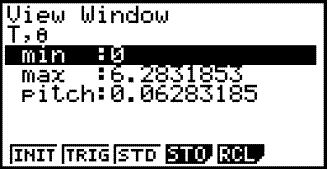Nå må vi stille inn tallene for t slik at vi får samme verdimengde som i tabellen over, altså fra -2 til + 2. Hvis vi setter pitch = 1, vil kurven se ut som den er sammensatt av korte linjer. Jo lavere pitch vi velger, jo "mykere" vil kurven se ut.

   Her skal det stå Min: -2, Max: 2. Pitch kan du for eksempel sette til 0,1.

For hver endring må du trykke for at den skal lagres.

Når vi er ferdig med innstillingene, går vi til grafmenyen.

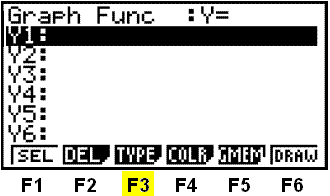
Vi må først velge typen graf (TYPE) med F3. Vi får opp en valgmeny nederst på skjermen.

Vi velger parameterform (Parm) ved å trykke på F3. Nå er grafmenyen på parameterform. Vi skriver inn likningen på parameterform (i gult på bildet).

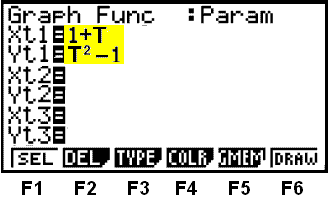
For å skrive T, trykker vi

Grafen skal se slik ut:

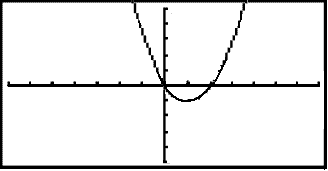
Eksempel 6

Vi skal se nærmere på denne likningen på parameterform:

x = 4 + 2 cos t y = 3 + 2 sin t

Vi multipliserer alle ledd med seg selv (kvadrerer), og bruker den viktige trigonometriske sammenhengen cos² t + sin² t = 1, til å kvitte oss med t.

Den øverste likningen gir oss x – 4 = 2 cos t  og  (x – 4)² = 4 cos²t.

Den nederste likningen gir oss y – 3 = 2 sin t  og  (y – 3)² = 4 sin²t.

Vi legger sammen likningene:

   (x – 4)² + (y – 3)² = 4 cos² t + 4 sin² t

                               = 4(cos² t + sin² t)

                               = 4

Vi står igjen med likningen (x – 4)² + (y – 3)² = 2² . Dette er likningen for en sirkel med radius 2 og sentrum i (4, 3).

Parameterfremstilling er bare en av mange måter å vise forholdet mellom x og y. Det finnes mange forskjellige koordinatsystemer. x - aksen og y - aksen trenger ikke nødvendigvis å være vinkelrette i forhold til hverandre, heller ikke å være i samme enhet.

Et mye brukt system er det polare koordinatsystemet. I et polart koordinatsystem er det bare en akse, denne tilsvarer den positive halvdelen av x - aksen. Endepunktet som tilsvarer 0 på x - aksen, kalles polen i dette systemet. Hvert punkt i koordinatsystemet representeres av en vinkel  q og avstanden r i forhold til polen. (se bildet)

Avstanden r har en retning, akkurat som en vektor. Den kan derfor være negativ. Hvis vinkelen q er i intervallet 0 < q < 180º, havner alle negative verdier av r under polaraksen. Vi måler vinkelen fra polaraksen og mot klokken, og vinkelen kan være negativ.

Vi kan også bruke polarkoordinater i et rettvinklet (kartesisk) koordinatsystem. Vi tenker oss da x - aksen som polaraksen, med pol i origo (0, 0).

Eksempel 7

Hva er polarkoordinatene til punktet (3, 4)?

Først tegner vi en tegning.

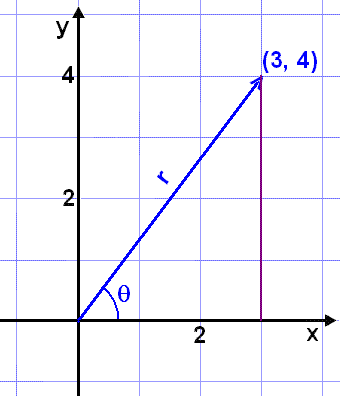
Vi kan finne r ved hjelp av Pythagoras.

   r² = 3² + 4² = 9 + 16 = 25

    r = 5

For å regne ut q, må vi bruke den trigonometriske sammenhengen at tan q = motstående side/hosliggende side. På denne måten kan vi regne ut vinkelen.

   q = tan^–1(4/3) 53,13º  0,93 rad.

Polarkoordinatene til punktet (3, 4) er altså (5; 0,93).

Eksempel 8

Regn ut de kartesiske koordinatene til punktet P, med polarkoordinatene (3, /4). Vi gjør som sist, og tegner opp koordinatsystemet.

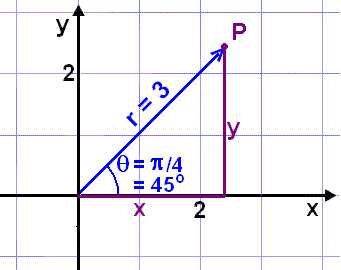
Vi bruker at cos q= nærliggende side/hypotenusen og at sin q = motstående side/hypotenusen.

   cos q = ^x/₃

          x = 3 cos 45º 2,12

    sin q = ^y/₃

          y = 3 sin 45º 2,12

Punktet P har de kartesiske koordinatene (2,12; 2,12).

Vi kan tegne opp polare koordinatsystemer der r og q må oppfylle visse vilkår. Hvis for eksempel q er fast, og r kan ha en hvilken som helst verdi, får vi en rett linje gjennom polen. Hvis det isteden er r som er fast og q kan være hva som helst i intervallet 0 < q < 2, er grafen en sirkel med midtpunkt i polen, og radius r.

Likninger på polar form skrives vanligvis på formen r = f(q).

Eksempel 9

Finn en likning med kartesiske koordinater, når vi har følgende likning med polarkoordinater:

    r = 4/(cos q – sin q)

Vi multipliserer først begge sider med (cos q + sin q), og bruker deretter reglene x = r cos q  og  y = r sin q.

   r (cos q – sin q) = 4

   r cos q – r sin q = 4

                    x – y = 4

                          y = x – 4

Likningen på polar form, r = 4/(cos q – sin q), tilsvarer likningen y = x – 4.

Eksempel 10

Finn en likning med kartesiske koordinater når likningen med polarkoordinater er slik:

    r = 2(cos q + sin q + 1/r)

Vi multipliserer begge sider med r for at likningen skal passe inn i formlene.

           r² = 2(r cos q + r sin q + 1)

   x² + y² = 2(x + y + 1)

   x² + y² = 2x + 2y + 2

Dette ligner på noe vi kjenner fra før.

      x² – 2x + y² – 2y = 2

Vi legger til 2 på begge sider av likhetstegnet.

   x² – 2x + 1 + y² – 2y + 1 = 2 + 2

   (x – 1)² + (y – 1)² = 2²

Dette er likningen for en sirkel med sentrum i (1, 1) og radiusen 2.

Eksempel 11

Nå skal vi se på grafen til likningen r = 5 sin 3q.

Vi kan prøve å konvertere likningen over til en x - y - likning, men det ser ikke så enkelt ut.

Vi skriver først om sin 3q.

   sin 3q = sin (2q + q)

Nå kan vi bruke addisjonssetningen, og deretter formelen for doble vinkler. Disse kan slås opp i en formelsamling.

   sin 3q = 3 sin q + 4 sin³ q

Vi kan nå skrive om likningen.

   r = 15 sin q + 20 sin³ q

Vi multipliserer begge sider med  r³ for å kunne bruke = r sin q.

   r⁴ = 15 r²·r sin q + 20 r³ sin³ q

       = 15 r² y + 20 y³

Nå kan vi bruke regelen r² = x² + y² og sette inn x² + y² istedenfor r².

                      r⁴ = 15 r² y + 20 y³

           (x² + y²)² = 15 (x² + y²)y + 20 y³

   x⁴ + 2x²y² + y⁴ = 15x²y + 15y³ + 20 y³

Nå har vi konvertert likningen, men resultatet ble en langt mer komplisert likning enn den vi begynte med. Vi kommer derfor til å bruke likningen med polarkoordinater når vi skal tegne grafen. Sett opp en verditabell.

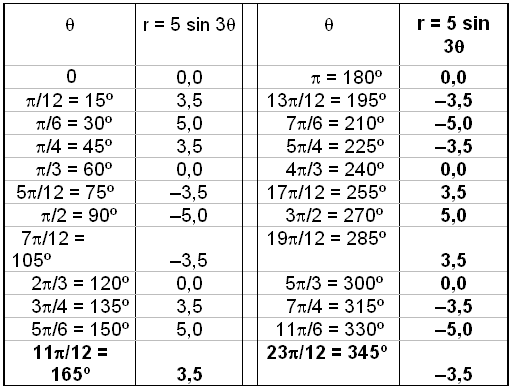
Tegn opp et koordinatsystem som ser ut som et spindelvev. Da blir det mye lettere å sette inn punktene fra verditabellen, og skissere grafen. Vi setter inn et punkt for hver vinkel, og r er avstanden fra polen.

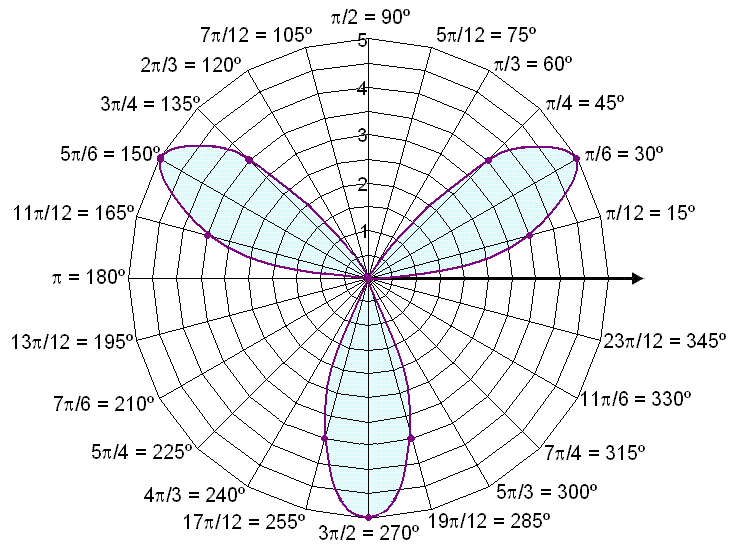
Grafen ser ut som et trekløver.

Vi kan også tegne grafen ved hjelp av en grafisk kalkulator.

Først må vi stille kalkulatoren inn på radianer. Åpne menyen med SHIFT og SET UP. Trykk på GRAPH, og deretter V-Window med .

Vi får opp en kjent meny:

Vi trenger ikke endre noe her, men trykker seks ganger på pil ned. Nå åpnes en ny meny.

Still inn kalkulatoren som på bildet. Minimum (min) skal være 0, og maximum (max) skal være. 6,2831853 (2). Nå kommer vinkelen til å anta alle mulige verdier mellom min og max, i en runde rundt polen. Vi går frem 2/100 av gangen.

Vi må trykke på for hver endring, så de lagres.

Når innstillingene er i orden, går vi til grafmenyen.

Vi velger TYPE (F3) for å få opp neste meny.

Vi velger alternativet r = med F2. Nå får vi muligheten til å skrive inn polarkoordinater i grafmenyen. Skriv inn som på bildet under (den gule linjen).

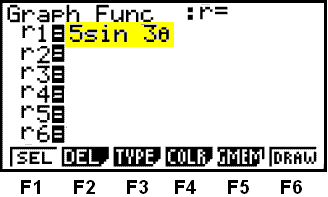
For å skrive inn  q, er det bare å trykke , fordi vi allerede har valgt å bruke polarkoordinater.

Grafen skal se slik ut:

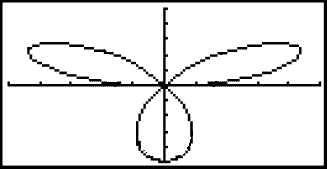
Øv på eksemplene, og regn deg gjennom Test 6 i Vektorer.

Husk å fylle ut sjekklisten underveis.