Brøk (addisjon og subtraksjon)
| © 2006 Rasmus ehf |
Brøk (addisjon og subtraksjon) |
|
Introduksjon 3.
1. Først må vi lage felles nevner.
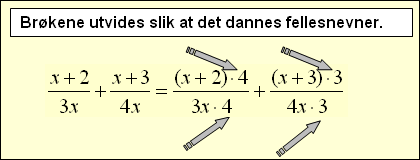
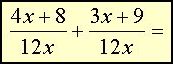
Når du har funnet felles nevner, arbeider du med tellerne og reduserer uttrykket ved først at samle like bokstavuttrykk og tall.
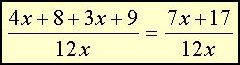Like bokstavuttrykk og tall
trekkes sammen.
2. Det er ofte nødvendig å omskrive brøken.
 |
||
 |
||
 |
Legg merke til at fortegnene endres når parentesen heves etter at uttrykkene er satt på felles brøkstrek. | |
 |
||
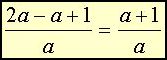3. En utdypning.
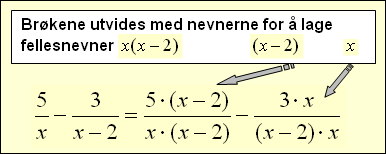
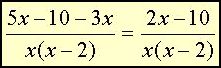Det er en betingelse
for disse brøkene, fordi nevneren
x(x - 2) må aldri bli lik 0.
Derfor gjelder at x < > 0 eller at x - 2 < > 0 og x(x - 2) < > 0 .
Tegnet < > betyr: " er ikke lik med ".
4. En ytterligere utdypning. Multiplikasjon av toleddet størrelse.
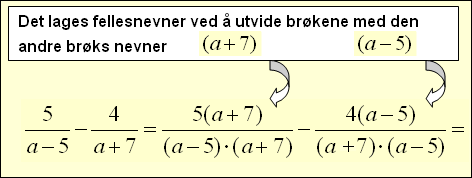
Nå trekker vi sammen ved først
å sette brøkene på felles brøkstrek, deretter
ganges det inn i parentesene og til sist reduseres uttrykkene
Her kan a verken være lik 5 eller -7, fordi nevneren da blir lik null.
Prøv nå å løse test3 i brøk. Hvis du får minst 80% riktige svar, har du fortjent å se deg i speilet og utbryte: "Så god jeg er i algebra"!