© 2006  Rasmus ehf

Funksjoner

  Print

Introduksjon 2.    Linjens ligning (lineære funksjoner).

( I et koordinatsystem, som beskriver en sammenheng mellom variabler, er variabelen y avhengig av variabelen x. En ligning som anvendes for å beskrive, hvordan noe er avhengig av noe annet, kalles for en funksjon. En funksjon, hvis graf er en rett linje, kalles en lineær funksjon. En lineær funksjon kan beskrives med formelen: y = ax + b, hvor a og b er en konstant. ) I en lineær funksjon er det tilstrekkelig å vite 2 punkter for at kunne tegne grafen (linjen). Man bør dog alltid bruke tre punkter for at kontrollere, at man har regnet riktig. Når man har en lineær funksjon kan det være hensiktsmessig å lage en tabell over de koordinater man regner ut.
 Sammenhengen mellom variablene skal være konstant, men man kan selv velge, hvilke tall man vil sette i stedet for x for så å regne ut y-koordinaten.
 Man velger selv hvor mange koordinatsett, man vil beregne. Man bruker  dog alltid minst tre punkter. Hvis punktene ikke ligger på en rett linje når de tegnes inn i i koordinatsystemet, kan man ved at kontrollere utregningene finne feilen.

Som eksempel prøver vi funksjonen: y = x + 1

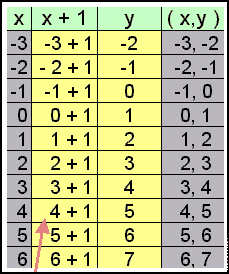
Tabell for y = x + 1

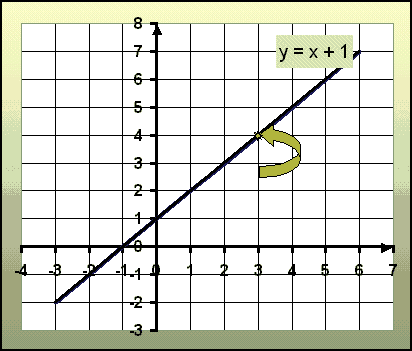
Grafen for y = x + 1
Eksempel:

x = 4 betyr at y = 4 + 1 = 5

Pile peker på punktet( 3, 4)

Man kan se pilen, som peker på punktet (3, 4). Dette er et eksempel på et punkt, som er hentet i tabellen. Et annet punkt finnes f.eks. på koordinatsettet (0, 1), som er det punktet, hvor grafen skjærer y - aksen. Når to punkt er avmerket i koordinatsystemet, er det lett å tegne linjen som går gjennom dem.

Andregradsfunksjoner

Funksjoner skrevet på en formel som: y = ax2 + b hvor a og b er kjente verdier,
kalles andregradsfunksjoner. For å kunne tegne en linje, som illustrerer denne type ligninger, er det nødvendig å kjenne flere enn tre punkt.

Eksempel: Funksjonen  y = x2 - 4  

Vi laver en tabell for x - verdier mellom -4 og +4.

Funksjonen: y = x2 - 4

Kurven:   y = x2 - 4

Eksempel: x = -4 betyr at

y = (-4)(-4) - 4 = 16 - 4 = 12
Som det kan ses, kan vi få samme y - verdi to ganger. Dette skyldes, at andregradsfunksjoner er symmetriske.

Punktet (4,12) motsvares med punktet (-4,12).
Legg merke til hvor kurven skjærer y - aksen og x - aksen.

Hvis man deler opp uttrykket   y = x2 - 4   i flere størrelser,

får man  y = x2 - 4 =(x-2)(x+2)

Hvis vi velger at y = 0, må x bli enten +2 eller -2 for at ligningen skal stemme.  

Hermed har vi koordinatene (-2,0) og (2,0).

Stigningstallet i en lineær funksjon.

Se på funksjonen y = 2x + 1.

Vi har funksjonen y = 2x +1. Stigningstallet 2 foran x viser hvor bratt linjen går. Det andre led d(tallet 1) viser hvor linjen skjærer y-aksen. 
Stigningstallet beregnes ved å dele forskjellen mellom to av linjens y - verdier med linjens tilsvarende x - verdier. Tegnet "delta" lar man ofte betegne en endring av en bestemt verdi.

y stiger fra +3 til +7, d.v.s. 7 - 3 = 4 enheter, mens x stiger fra +1 til +3, d.v.s. 3 - 1 = 2 enheter. Stigningstallet for grafen er 2, hvilket svarer til tallet foran x. Man kan også beregne stigningstallet ved å tegne en rettvinklet trekant ved linjen og dele den loddrette sides lengde med den vannrette sides lengde.

Gå nå til test 2 i Ligningssystemet.