Introduksjon 3.

Ligninger og kurver og skjæringspunktet for to linjer.

Har man to ligninger med to ukjente, er der minst tre metoder for å finne linjenes skjæringspunkt.

Metode 1: Å løse ligningene grafisk.

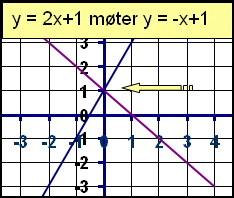
Vi ser på ligningene I: y = 2x + 1 og II: y = -x + 1

Først lager vi en tabell for hver ligning.

Har man funnet de koordinatsett som linjene har felles, har man funnet linjenes skjæringspunkt.  Vi tegner begge linjene y=2x + 1 og y = -x + 1. Linjene skjærer hverandre i punktet ( 0, 1).Linjene vil skjære hverandre i et punkt, idet de har forskjellig stigningstall. Linjer med lik stigningstall er parallelle og skjærer ikke hverandre.

Metode 2: Addisjonsmetoden.

Man kan beregne skjæringspunktene ved å addere de to ligninger leddvist.
I: y = 2x +1

II: y = -x + 1

Vi begynner med en omskrivning.

I: -2x + y = + 1                                

II: x + y = 1  

Vi ganger ligning II med  2 på begge sider av likhetstegnet

Herved fås 2(x + y = 1)  eller  2x + 2y = 2

Vi adderer.

I:     -2x + y = 1

II:    2x + 2y = 2

        0  + 3y = 3 

Dermed får vi at y = 1  Denne verdi for y innsettes i ligning  I: 

Da blir 1 = 2x + 1   Hermed har vi en alminnelig ligning med en ukjent, og den løses på vanlig måte:  

 I: +1 -1 = 2x  eller 0 = 2x

Altså x = 0.

Dette resultat (x, y) = (0,1) passer fint med den grafiske løsning. Punktet (0,1) er det eneste felles punkt på de to linjene.

Metode 3 : Innsetningsmetoden.

Uttrykkene kan kun ha samme koordinater i det punkt, hvor de skjærer hverandre.
Derfor kan man være sikker på, at y i ligning I har samme verdi som y i ligning
II i nettopp dette punkt.

I: y = 2x +1

II: y = -x + 1

Da y-verdiene er like når linjene skjærer hverandre er y = y  og derfor også  -x + 1 = 2x + 1   

Dette er en helt vanlig ligning med en ukjent, og skal løses som en sådan.

-x - 2x = 1 - 1 eller - 3x = 0

Dette betyr at  x = 0. Denne verdi for x kan så innsettes i ligning I.  

y = 2x + 1 = 0 + 1 = 1

D.v.s. linjenes skjæringspunkt er  (0,1).

Gjør nå  test 3 i Ligningssystemet.