Repetition af algebra
| © 2005 Rasmus ehf |
Repetition af algebra |
|
Introduktion.
Her følger nogle repetitionsopgaver i algebra, som det kan være gavnligt at øve sig lidt på. I matematikhjælpen findes der lignende opgaver, som du kan tage fat i , hvis du har behov for forklaringer.
Exempel 1: Beregn potensen og reducer udtrykket
36 + 2·8=
36 + 16 = 52
Exempel 2: Forkort udtrykket
y + xy +2y= 3y + xy
Exempel 3: Forkort udtrykket
xy +yx = 2xy
Exempel 4: Forkort udtrykket
Exempel 5: Forkort udtrykket
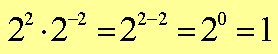
Exempel 6: Forkort udtrykket så meget som muligt
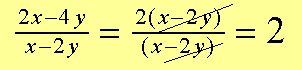
Se Flerleddede størrelser og Brøk: Multiplikation og Division.
Exempel 7: Forkort udtrykket så meget som muligt
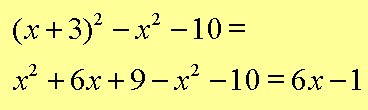
Exempel 8: Forkort udtrykket så meget som muligt
x +14 = 30
x = 30 - 14
x = 16
Exempel 9: Forkort udtrykket så meget som muligt
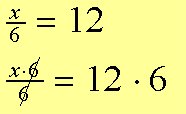
x = 72
Exempel 10: Forkort udtrykket så meget som muligt
5(x + 2) = - (8 - 3x)
5x + 10 = - 8 + 3x
5x -3x = -8 -10
2x = -18
x = -9
Exempel 11: Beregn udtrykket når a=3.
21 - 36 = -15 Se Fortegn.
Exempel 12: Forkort udtrykket så meget som muligt
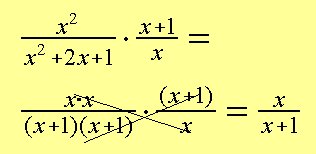
Se Brøk: Multiplikation og Division. og flerleddede størrelser.
Exempel 13: Forkort udtrykket så meget som muligt
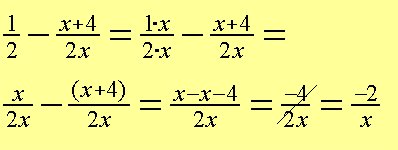
Exempel 14: Løs ligningen
Exempel 15: Løs ligningssystemet for mulige værdier for x og y:
Alternativ 1:
Se flerleddede
størrelser og ligningssystemet
(x - y)(x + y)=3·5
Da får vi udtrykkene
a) x - y = 3
b) x + y = 5 Vi lægger udtrykkene sammen og får så:
x + x + y - y = 3 + 5
2x=8 altså er x = 4
Vi sætter værdien 4 ind for x i ligningen og ser at:
4 + y = 5
y = 5 - 4
y =1
Alternativ 2:
(x - y)(x + y)=1·15
Da får vi udtrykkene
a) x - y = 1
b) x + y = 15 Udtrykkene lægges sammen og herved får vi:
x + x + y - y = 1 + 15
2x=16 altså er x = 8
Dette indsættes i ligningen på x`s plads:
8 + y = 15
y = 15 - 8
y = 7
Nu kan du forhåbentligt trygt gå I gang med den store prøve, som du har forberedt dig til med de foregående tests.
Held og lykke!
