© 2000-2012 Rasmus ehf og Jóhann Ísak Pétursson
Funktioner I
|
© 2000-2012 Rasmus ehf og Jóhann Ísak Pétursson |
Funktioner I |
|
Introduktion 5
Funktions
definitionsmængde og værdimængde
Vi kan forestille os en
funktion, som om det var en maskine eller en række handlinger udført på tal.
Tallene der puttes i maskinen kaldes definitionsmængden og tallene der kommer ud
kaldes værdimængden.
Definitionsmængden for en funktion er den mængde af gyldige værdier, som man kan
sætte ind i funktionen. Funktionen f's definitionsmængde skrives som Dm(f).
Hvis funktionen kan tage alle værdier, så er definitionsmængden mængden af alle
reelle tal (mængde R).
Værdimængden for en funktion er den mængde af værdier, som en funktion er i
stand til at returnere.
Funktionen f's værdimængde skrives som Vm(f).
Tallene i definitionsmængden er x-værdien og tallene i værdimængden er
y-værdien.
Vi har set at nogle funktioner ikke accepterer alle x-værdier, så mulighederne
for definitionsmængden er begrænsede. Da x-værdien bestemmer y-værdien, så er
værdimængden også begrænset.
Det er forholdsvis nemt at bestemme definitionsmængden, da vi kun skal forholde
os til hvilke x-værdier vi ikke kan bruge i vores udregninger.
Der er to almindelige udregningsmetoder der begrænser valgmulighederne af
x-værdier:
1. Man kan ikke dividere med 0.
2. Man kan ikke tage kvadratroden af et negativt tal.
Det kan være mere besværligt at finde funktionens værdimængde. Den nemmeste måde
er at studere grafen for funktionen. Vi kan også se på funktionstabellen, vælge
ekstreme værdier for x og prøve at se hvilket værdi y får.
Eksempel 1
Lad os se på funktionen f(x) = 2x + 4
Når vi laver en funktionstabel og vælger hvilken som helst værdi for x, så ser
vi at y tager alle reelle værdier. Jo større x-værdi vi vælger, desto større vil
y-værdien blive. Når vi tegner grafen, kan vi se at det er en lige linje, som vi
kan forlænge uendeligt i begge retninger. Så værdimængden er også R. Vm(f) = R.
|
Definitionsmængde |
Værdimængde |
|
|
f(x) = 2x + 4 |
||
|
X |
eller y = 2x + 4 | |
| -2 | 0 | |
| -1 | 2 | |
| 0 | 4 | |
| 1 | 6 | |
| 2 | 8 |
Eksempel 2
Lad os nu se på funktionen
![]()
|
Definitionsmængde |
Værdimængde |
|
| x | f(x) = 1/x2 | |
| -2 | 1/4 | |
| -1 | 1 | |
| -1/2 | 4 | |
| 0 | umuligt | |
| 1/2 | 4 | |
| 1 | 1 | |
| 2 | 1/4 |
Den eneste værdi vi ikke kan vælge er x=0, fordi så skulle vi dividere med 0.
Definitionsmængden er derfor R\{0}.
Det er ikke nemt at se hvilke værdier y får, ved at kigge på funktionstabellen.
Til gengæld kan vi se at
f(10) = f(−10) = 1/100 and f(100) = f(−100) = 1/10.000 osv.
Eftersom x bliver større, så kommer y tættere og tættere på 0.
Dog bliver y aldrig lige med 0 eller et negativt tal.
Når x kommer tættere og tættere på 0, bliver y større og større:
f(1/10) = f(−1/10) = 100 og
f(1/100) = f(−1/100) = 10.000.
Konklusionen er at værdimængden er alle reelle tal større end 0. Vm(f) =
![]() 0,
0,
![]()
![]() .
.
Eksempel 3
Lad os se på funktionen
![]()
| Definitionsmængde |
Værdimængde |
|
|
x |
||
| -2 | -4¼ | |
| -1 | -3½ | |
| 0 | -2½ | |
| 1 | -2 | |
| 1½ | -2½ | |
| 2½ | 2½ | |
| 3 | 2 | |
| 4 | 2½ | |
| 5 | 3½ |
Vi kan bruge alle tal, undtaget x=2, så definitionsmængden er Dm(f)= R\{2}.
Af grafen og funktionstabellen kan vi se at y kan tage alle værdier, undtaget dem mellem –2 og 2.
Vm(f) =
{y
![]() R│y
R│y
![]() −2 eller y
−2 eller y
![]() 2}.
2}.
Eksempel 4
Lad os nu se på parablen y = x2 − 2x + 2
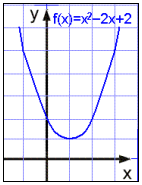
Vi ved at den vender opad fordi a > 0 og derfor er toppunktet en minimal værdi.
Vi finder symmetriaksen med formlen
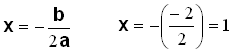
Det næste vi gør er at finde y-værdien når x = 1.
f(1) = 1 − 2×1 + 2 = 1. Toppunktet er derfor (1, 1) og Vm(f) =
Eksempel 5
Find værdimængden til funktionen
![]()
| Definitionsmængde |
Værdimængde |
 |
|
X |
||
| -11 | 4 | |
| -4 | 3 | |
| 1 | 2 | |
| 4 | 1 | |
| 5 | 0 | |
Vi kan se at x ikke kan blive større end 5, fordi det betyder at vi skal tage kvadratroden af et negativt tal. Til gengæld kan vi vælge hvilket som helst negativt tal for x (fordi så får vi to minusser foran x (−− = +) under kvadratroden). Definitionsmængden er:
Dm(f)
=
{x
![]() R│x
R│x
![]() 5}, Dm(f)
=
5}, Dm(f)
=
![]()
![]() , 5
, 5
![]()
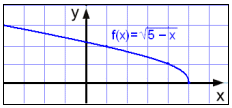
For at finde værdimængden skal vi lave en funktionstabel og se på grafen.
Vi ser at grafen ender i punktet (5, 0), men fortsætter op mod venstre så længe vi ønsker at tegne den. y-værdien bliver aldrig mindre end 0. Værdimængden er derfor:
Vm(f) =
{y
![]() R│y
R│y
![]() 0},
Vm(f)
=
0},
Vm(f)
=
![]() 0,
0,
![]()
![]() .
.
Husk: Tallene i definitionsmængden er x-værdien og tallene i værdimængden er y-værdien.
Prøv test 5 i Funktioner I.
Husk at bruge din tjekliste.