Matematikhjælpen - Mængdelære - Intro 3

Mængdelære

Introduktion 3 Reelle tall

Vi forestiller os en tallinie (x–aksen) som en sammenhængende række af punkter. Hvert punkt betegner sin afstand til nul. Vi bruger det negative fortegn (-) når punktet er til venstre for nul, og det positive fortegn (+), når punktet er til højre for nul.

Talmængderne N og Z er ikke de eneste talmængder på linien. De indeholder bare nogen af punkterne

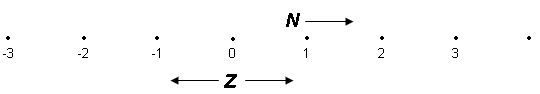
Mængden af rationale tal Q findes også på linien, men tallinien indeholder også mange andre tal. Der findes uendelig mange tal mellem dem vi allerede har nævnt, som ikke kan skrives som brøker og som derfor ikke er med i de mængder, vi hidtil har omtalt.

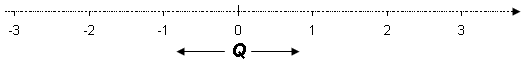
Disse ikke omtalte tal kaldes de irrationale tal. De er kendetegnet ved at have et uendeligt antal decimaler efter komma, men decimalerne gentager sig ikke, og er derfor ikke periodiske. Her er nogle eksempler:

0,909009000900009
0,123456789101112
	= 1,41421356237
	= 1,73205080756
	= 3,141592653589

De irrationale tal danner sammen med Q (som indeholder mængderne Z og N) den sammenhængende tallinie, som vi kalder den reelle tallinien. Den reelle tallinie indeholder mængden af reelle tal R.

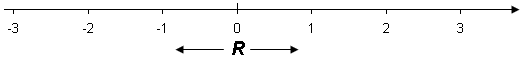
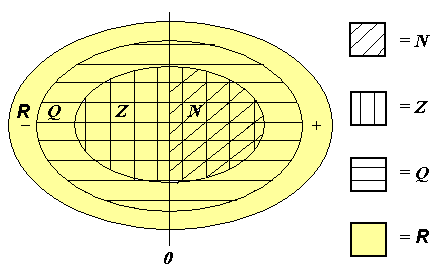
Det følgende diagram viser forholdet mellem mængderne R, Q, Z og N. Mængden R indeholder alle de andre mængder, og kan deles op i rationale- og irrationale tal. Den del af diagrammet, som ingen markering har, indeholder de irrationale tal. Den del af diagrammet, som har vandrette linier, udgør de rationale tal (mængden Q). Mængden Q indeholder hele tal (Z) og brøker som ikke er hele tal. Endelig kan Z inddeles i hele, positive tal N og hele negative tal, begge dele med og uden nul.

Vi kan beskrive intervaller på den reelle tallinie på forskellige måder. For eksempel kan intervallet mellem 1 og 5 være inklusive 1 og 5, og så skrives det på følgende måde:

Som ulighedt: 1 x 5

Som mængdenotering: { x R | 1 x 5 }

Som diagram:

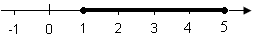
En anden måde er ved at bruge intervalparenteser. Ovennævnte eksempel kan skrives som:

[1; 5] eller [1, 5] (lærebogssystemerne kan have forskellige variationer)

Et interval som [1; 5] hvor både 1 og 5 er inkluderet, kaldes et lukket interval.

Vil man skrive et udtryk for et interval mellem to tal, hvor begge tal ikke er inkluderet, skriver man det anderledes.

Lad os tage eksemplet, hvor tallene er større end 1, men mindre end 5

Som ulighed: 1 < x < 5

Som mængdebetegnelse: { x R | 1 < x < 5 }

Som diagram

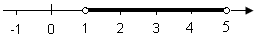
I intervalparentes

eller [1,5] (lærebogssystemerne kan have forskellige variationer)

Læg mærke til, at der bruges andre cirkler (åbne cirkler) til at markere, at endetallene 1 og 5 ikke er med.

Intervalparentesen og også ændret sig. Intervallet ]1;5[ betyder, at hverken endetallet 1 eller 5 er inkluderet. Vi taler her om et åbent interval.

Til sidst skal vi se på intervaller, hvor det ene endetal er med og det andet ikke.

For eksempel kan vi se på det interval, hvor x er større eller lige med 1 og mindre end 5

Som ulighed: x ≥ 1

Som mængdebetegnelse: { x R | x ≥ 1 }

Som diagram:

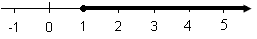
Som intervalparentes: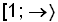

eller [1, ∞[ (lærebogssystemerne kan have forskellige variationer)

Denne type interval kaldes halvåben. Halvåbne intervaller går ikke altid uendelig langt ud til en af siderne.

Her er f. eks intervallet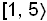

hvor 1 er inkluderet men 5 er det ikke, vist som diagram.

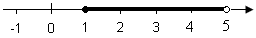
Prøv nu test 3 i mængdelære.

Husk at overføre resultatet til din checkliste.