st10k02

( I et koordinatsystem som beskriver en sammenhæng mellem variabler er variablen y afhængig af variablen x. En ligning som anvendes for at beskrive, hvordan noget er afhængigt af noget andet, kaldes for en funktion. En funktion, hvis graf er en ret linie, kaldes en lineær funktion. En lineær funktion kan beskrives med formlen : y = ax + b, hvor a og b er kendte faktorer. )

I en lineær funktion er det tilstrækkeligt at kende 2 punkter for at kunne tegne grafen (linien). Man bør dog altid bruge tre punkter for at kontrollere, at man har regnet rigtigt. Når man har en lineær funktion kan det være hensigtsmæssigt at lave en tabel over de koordinater, man regner ud.

Sammenhængen mellem variablerne skal forblive konstant, men man kan selv vælge, hvilke tal man vil sætte i stedet for x for bagefter at regne y-koordinatet ud.

Man vælger selv hvor mange koordinatsæt, man vil beregne. Man anvender dog altid mindst tre punkter. Hvis punkterne ikke ligger på en ret linie når de indsættes i koordinatsystemet, kan man ved at kontrollere udregningerne finde fejlen.

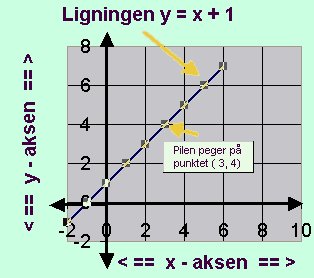
Tabel for y = x + 1	Grafen for y = x + 1
Eksempel: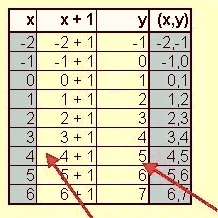
x = 4 betyder at y = 4 + 1 = 5	Pilen peger på punktet ( 3, 4)

Man kan se pilen, som peger på punktet (3, 4). Dette er et eksempel på et punkt, som er hentet i tabellen. Et andet punkt findes f.eks. på koordinatsættet (0, 1), som er det punkt, hvor grafen skærer y - aksen. Når to punkter er afmærket i koordinatsystemet, er det let at tegne den linie, der går gennem dem.

Funktioner skrevet på en formel som: y = ax² + b hvor a og b er kendte værdier,
kaldes andengradsfunktioner.

For at kunne tegne en linie, der illustrerer denne type ligninger, er det nødvendigt at kende flere end tre punkter.

Funktionen: y = x² - 4	Kurven: y = x² - 4

Eksempel: x = -4 betyder at y = (-4)(-4) - 4 = 16 - 4 = 12	Som det kan ses, kan vi få samme y - værdi to gange. Dette skyldes, at andengradsfunktioner er symmetriske.

Punktet (4,12) modsvares med punktet (-4,12).
Læg mærke til hvor kurven skærer y - aksen og x - aksen.

Hvis vi vælger at y = 0, må x blive enten +2 eller -2 for at ligningen skal stemme. Hermed har vi koordinaterne (-2,0) og (2,0).

Vi har funktionen y = 2x +1. Koefficienten 2 foran x viser hvor stejlt linien hælder. Det andet led (tallet 1) viser hvor linien skærer y-aksen.
Hældningskoefficienten beregnes ved at dele forskellen mellem to af liniens y - værdier med liniens tilsvarende x - værdier. Tegnet "delta" lader man ofte betegne en ændring af en bestemt værdi.

y stiger fra +3 til +7, d.v.s. 7 - 3 = 4 enheder, mens x stiger fra +1 til +3, d.v.s. 3 - 1 = 2 enheder. Hældningskoefficienten for grafen er 2, hvilket svarer til koefficienten foran x. Man kan også beregne hældningskoefficienten ved at tegne en retvinklet trekant ved linien og dele den lodrette sides længde med den vandrette sides længde.