Geometri
| © 2005 Rasmus ehf |
Geometri |
Introduktion 5.
Arealer:
Enheder for areal:
| km2 | hm2 | dam2 | m2 | dm2 | cm2 | mm2 |
| 1 | 00 | 00 |
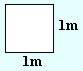
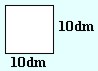
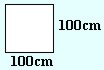
| 1m2 = 100dm2 = 10000cm2 |
 |
|
 |
|
 |
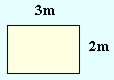
Du har beregnet arealet for bestemte figurer, f.eks.:
 |
||
| A = | ||
A = seks kvadratmeter.
Hvis du skal angive svaret i kvadratcentimeter, kan du anvende tabellen for arealenheder:
| km2 | hm2 | dam2 | m2 | dm2 | cm2 | mm2 |
| 6 | 00 | 00 |
| 6m2 = 60000cm2 |
En anden god måde at løse opgaven på er ved at forandre meterenheden til centimeter inden udregningen:
 =
=
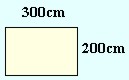
|
A = |
|
Samlet overflade af en kasse. Du skal beregne arealet af alle seks sider.
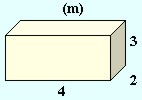 |
||
![]()
Dette var kun tre af siderne. Kassen har tre andre sider der er præcis lige så store. Det samlede areal bliver derfor:
![]()
For at kunne beregne samlet overflade af en figur, må vi kende figurens sider og bagefter beregne.
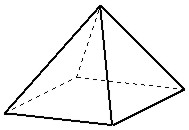
| Samlet overflade af en pyramide = | rektanglets areal + fire trekanters arealer. |
|
Samlet overflade af en pyramide = |
 + + + + + + + + |
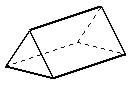
| Arealet af et prisme = |  +
+  +
+  +
+  +
+  |
Den krumme overflade
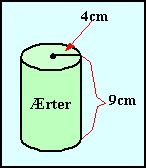
| Samlede overflade af en cylinder ( en konservesdåse) = | 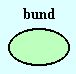 +
+  +
+  |
den krumme overflade ( etiketten) |
| Lågets areal | |
| Bundens areal | Samme areal som låget |
Den krumme overflade bredes ud så det får form som et rektangel ( etiketten rulles ud ) :
 |
|
| Denne
side svarer til cirklens
omkreds.
|
|
Dåsens ( cylinderens) samlede overflade. |
 |
| A = |
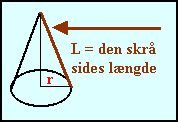 |
Arealet af en kegles krumme overflade = |
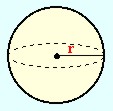 |
Arealet af en kugle = |
Sæt dig grundigt ind i dette kapitel og udfør herefter test 5 i geometri: