© 2007 Rasmus ehf og Jóhann Ķsak
© 2007 Rasmus ehf og Jóhann Ķsak |
Hornaföll |
|
Skošum rétthyrndan žrķhyrning meš langhlišina 1.
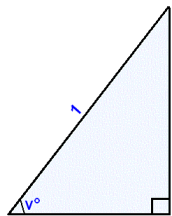 |
Mótlęg skammhliš = sin v° |
Ašlęg skammhliš = cos v° |
Skilgreiningin į sķnus var
sin v° = mótlęg skammhliš/langhliš
og skilgreiningin į kósķnus var
cos v° = ašlęg skammhliš/langhliš.
Ef langhlišin er 1 žį er gildir aš
sin v° = mótlęg skammhliš og cos v° = ašlęg skammhliš.
Viš skulum nś skoša hring ķ hnitakerfinu. Hann į aš hafa mišju ķ (0, 0) og hafa radķus 1, en žannig hringur er nefndur einingarhringur.
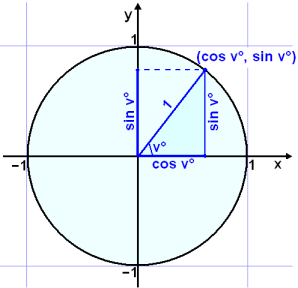
Teiknum horniš v° ķ hringinn žannig aš annar armur žess verši į x-įsnum og hinn myndi radķus hringsins (meš lengdina 1) eins og myndin sżnir. Žį kemur fram žrķhyrningur meš langhlišina 1 žannig aš skammhlišarnar eru cos v° og sin v°. Viš sjįum aš hornpunkturinn į hringnum hlżtur aš hafa hnitin (cos v°, sin v°).
Skošum nś tan v° į sama hįtt.
 |
Mótlęg |
Ašlęg skammhliš = 1 |
Skilgreiningin į tangens var
tan v° = mótlęg skammhliš/ašlęg skammhliš.
Ef ašlęga skammhlišin hefur lengdina 1 žį er
tan v° = mótlęg hliš.
Teiknum žetta upp ķ einingarhringinn.
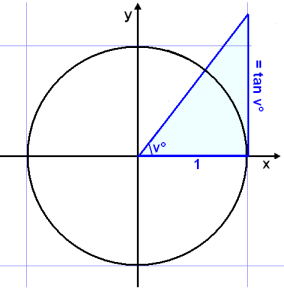
Viš getum nś gert eftirfarandi śtreikninga:
mótlęg skammhliš
tan v° =![]()
ašlęg skammhliš
mótlęg skammhliš/langhliš |
Hér deilum viš fyrir ofan og nešan meš langhlišinni. |
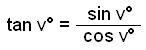
Žessar athuganir okkar į hornaföllum ķ einingarhringnum gilda fyrir horniš v° sem liggur upp og til vinstri frį x-įsnum. Hugsum okkur horniš v° verša til viš snśning um nśllpunktinn į žeim armi hornsins sem ekki er į x-įsnum. Žessi stefna (upp og til vinstri eša rangsęlis) er skilgreind sem jįkvęšur snśningur og gagnstęš stefna sem neikvęšur snśningur. Fęrsla punktsins P upp og til vinstri frį x-įsnum eftir einingarhringnum er jįkvęšur snśningur (sjį mynd).
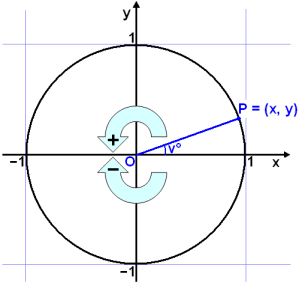
Viš getum nś śtvķkkaš skilgreininguna hornafallanna į eftirfarandi hįtt:
cos v° = x-hnit punktsins P sin v° = y-hnit punktsins P |
Žessi skilgreining sżnir okkur aš hornaföllin hafa mismunandi formerki eftir žvķ ķ hvaša fjóršung hnitakerfisins radķusinn OP vķsar.
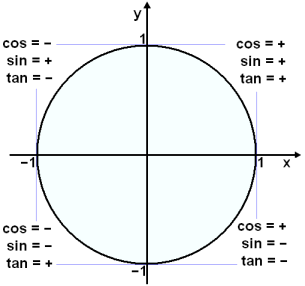
Ef viš hugsum okkur aš punktur fęrist ķ jįkvęša stefnu eftir hringnum žį endurtaka kósķnus og sķnus sig į 360° fresti en tangens endurtekur sig į 180° eins og kemur ķ ljós ķ sżnidęmi 4.
Reiknum hvaša jįkvęšu stefnu −200° samsvara.
Hér skulum viš bęta viš einum hring eša 360°.
−200° + 360° = 160°
Skrifum 1100° sem horn į bilinu 0°
![]() v° < 360°.
v° < 360°.
Hér žurfum viš aš draga frį nokkra heila hringi.
1 hringur: 1∙ 360° = 360°
2 hringir: 2∙ 360° = 720°
3 hringir: 3∙ 360° = 1080°
Viš žurfum ekki hęrra.
1100° − 1080° = 20°
Notum Pżžagórasarreglu til žess aš reikna nokkur nįkvęm gildi į hornaföllunum.
Fyrsti möguleikinn er 30° en žį er mótlęga skammhlišin (sin 30°) helmingur af langhlišinni eša ½.
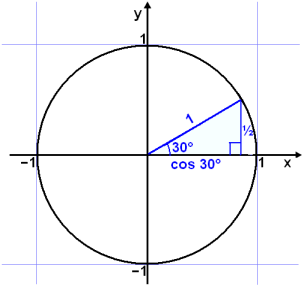 |
sin 30° = ½ = 0,5 cos 2 30° + (½)2 = 12 cos 2 30°= 1 − ¼ = ¾
≈ 0,866 |
Regla Pżpagórasar |
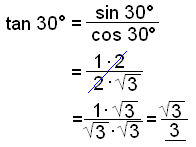
≈ 0,577
Nęsti žrķhyrningur sem viš getum reiknaš śt
er meš 45° horni og tvęr jafn
langar skammhlišar sem viš getum kallaš a.
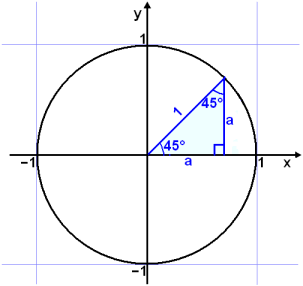 |
a2 + a2 = 1 2a2 = 1 a2 = ½ |
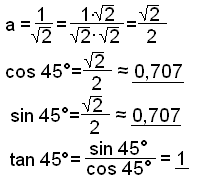 |
Žį er žaš 60° horniš.
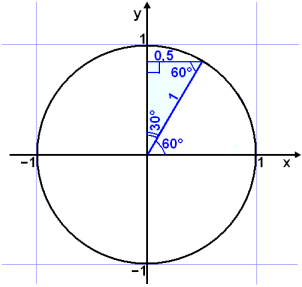 |
Viš fįum aftur žrķhyrning meš 30°, 60° og 90° hornum og getum nżtt okkur śtreikningana hér fyrir ofan. Nś hefur sķnus tekiš gildi kósķnuss og öfugt. |
 |
Hornaföllin fyrir 90° horn getum viš lesiš beint af einingarhringnum. Armur hornsins fellur saman viš y-įsinn žannig aš x-hnitiš er 0 og y-hnitiš er 1.
cos 90° = 0
sin 90° = 1
tan 90° = 1/0 er ekki til.
Žį er nęst 120° horniš (90°+ 30°) og aftur fįum viš 30°, 60° og 90° žrķhyrning.
 |
Hér erum viš vinstra megin viš y-įsinn žannig aš kósķnus er neikvęšur. |
 |
Žannig getum viš haldiš įfram aš reikna.
135° horniš (90°+ 45°) hefur t.d. samsvarandi hornaföll og 45° horniš en formerkin verša önnur.
Reiknum hornaföllin fyrir 225° horn.
Žetta er 45° meira en 180° (45° + 180° = 225°). Viš fįum žvķ eftirfarandi žrķhyrning:
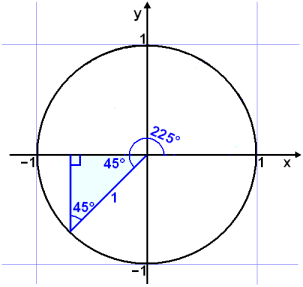 |
Viš getum reiknaš žetta eins og ķ sżnidęmi 3 en nś eru bęši kósķnus og sķnus neikvęšir. Tangens hins vegar veršur jįkvęšur (− deilt meš −). |
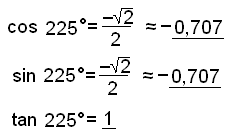 |
Tökum eftir žvķ aš tangens endurtekur sig nś eftir 180° og aftur oršinn 1 eins og tan 45°.
Finnum allar lausnir į jöfnunni tan x° = 2 og sķšan žęr lausnir sem eru į bilinu 0° £ x° < 360°.
Notum andhverfa falliš viš tan x į reiknivélinni.
tan −1(2) ≈ 63,44°
Nś vitum viš aš tangens endurtekur sig į 180° fresti žannig aš viš getum nįš yfir allar lausnir meš žvķ aš bęta viš k∙180° žar sem k er heil tala. Svariš er žvķ eftirfarandi:
x° ≈ 63,44° + k∙180° k er heil tala.
Žetta gefur lausnirnar x° ≈ 63,44° og x° ≈ 63,44° + 180° ≈ 243,44° į bilinu 0° £ x° < 360°.
Finnum nś hvenęr sinus tekur gildiš 0,5.
Skošum fyrst sin v° = 0,5. Reiknivélin gefur sin −1(0,5) = 30° en skošum žetta nįnar.
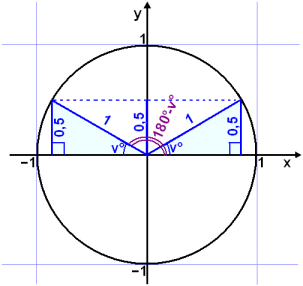
Ķ dęminu er gefin hęšin 0,5 upp eftir y-įsnum (sin v° = 0,5). Viš žurfum sem sagt aš finna hvaša tvö horn koma fram žar sem lįrétt lķna ķ hęšinni 0,5 sker einingarhringinn (sjį brotnu lķnuna į myndinni). Viš getum teiknaš tvo eins žrķhyrninga sem bįšir hafa horniš v° (= 30°) og mótlęga hliš 0,5 (= sin 30°). Horniš sem reiknivélin fann er minnsta horniš frį jįkvęša x-įsnum en žaš er bara annaš svariš. Hitt svariš er v° (eša 30°) til baka frį stefnu neikvęša x-įssins eša 180° − 30° = 150°.
Viš sjįum af sżnidęmunum hér fyrir ofan aš eftirfarandi regla gildir:
| sin v° = sin (180°-v°) |
Žessa reglu notum viš žegar viš leysum jöfnur af geršinni
sin v° = a
Reiknivélar gefa ašeins eina lausn sem er minnsta horniš frį jįkvęša x-įsnum. Hitt horniš finnum viš meš žvķ aš draga lausnina sem reiknivélin gefur frį 180°. Sķšan žurfum viš aš bęta k∙360° viš bįšar lausnirnar ef viš viljum sżna allar lausnir.
Finnum allar lausnir į jöfnunni sin v° = −0,6.
Teiknum žetta upp til žess aš sjį hvaš gera skal.
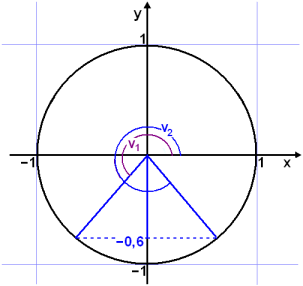
Reiknivélin gefur sin −1(−0,6) ≈ −36,9°.
Drögum žaš frį 180°.
180° − (−36,9°) ≈ 216,9°
Bętum einum hring viš −36,9° til žess aš losna viš mķnusinn śr svarinu.
−36,9° + 360° ≈ 323,1°
Svörin verša: v1 ≈ 216,9° + k∙360° og v2 ≈ 323,1° + k∙360°
Leysum jöfnuna cos v° = 0,7.
Teiknum žetta upp. Žaš er góš regla sem sżnir hvaša svör koma til greina.
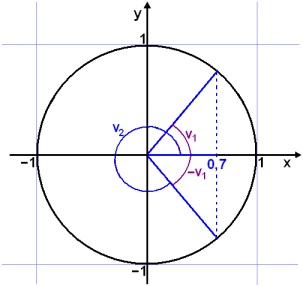
Gefiš er aš fjarlęgšin frį y-įsnum er 0,7. Lóšrétt lķna ķ gegnum 0,7 sker einingarhringinn į tveimur stöšum. Reiknivélin gefur cos −1(0,7) ≈ 45,57°. Viš sjįum nś af myndinni aš hinn skuršpunkturinn kemur fram ķ −45,57° og til žess aš fį jįkvęša grįšutölu žurfum viš aš bęta viš 360°.
Lausn: v1 ≈ 45,57° + k∙360°
v2 ≈ −45,57° + 360° + k∙360° ≈ 314,43° + k∙360°
Viš sjįum af sżnidęminu hér fyrir ofan aš eftirfarandi regla gildir:
| cos v° = cos(-v°) |
Žessa reglu notum viš žegar viš leysum jöfnur af geršinni
cos v° = a
Reiknivélar gefa eina lausn sem er horniš frį jįkvęša x-įsnum. Hin lausnin er žetta horn meš neikvęšu formerki. Viš bįšar lausnirnar žurfum viš sķšan aš bęta k∙360° ef viš viljum sżna allar lausnir.
Leysum ójöfnuna cos v° < −0,7 į bilinu 0° £ v° < 360°.
Leysum fyrst jöfnuna cos v° = −0,7.
Reiknivélin gefur cos −1(−0,7) ≈ 134,43° og hin lausnin er žį −134,43° + 360° ≈ 225,57°. Nś getum viš teiknaš žetta upp ķ einingarhringinn.
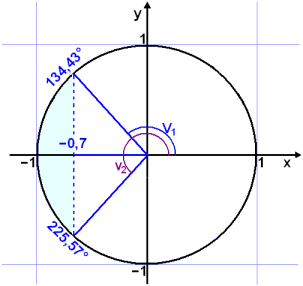
Viš sjįum af myndinni aš cos v° er fyrir nešan −0,7 ef v° er į litaša bilinu į myndinni. Lausnin er 134° < v°< 226°.
Ęfšu žig į žessum ašferšum og taktu sķšan próf
2 ķ hornaföllum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum