© 2007 Rasmus ehf og Jóhann Ķsak
© 2007 Rasmus ehf og Jóhann Ķsak |
Hornaföll |
|
Viš skulum nś skoša gröf hornafallanna og byrjum į fallinu f(v°) = sin v°. Horniš v° er męlt frį x-įs hnitakerfisins og er stašsett ķ einingarhring og viš hugsum okkur aš žaš fari stöšugt stękkandi.
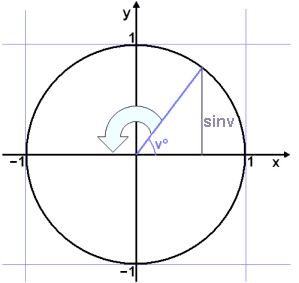
Setjum upp gildistöflu:
Viš höfum įšur reiknaš śt sin 30° og sin 60° meš žvķ aš nota okkur aš žrķhyrningur meš 30°, 60° og 90° horn hefur skammhliš sem er helmingur af langhlišinni og nota sķšan reglu Pżžagórasar. Viš getum žvķ aušveldlega reiknaš sin v° į 30° fresti. Einnig getum viš notaš sin x falliš į reiknivélum eša ķ töflureiknum.
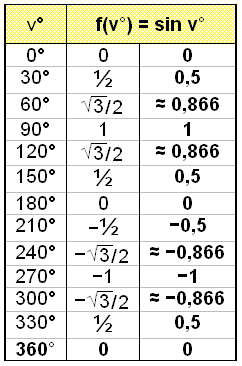
Viš skulum nś setja žetta upp ķ graf.
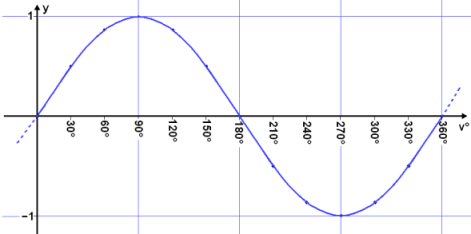
Nišurstašan er hin žekkta sķnusbylgja sem er eins konar stęršfręšilegur grunnur fyrir margs konar nįttśrulega bylgjur. Gallinn viš aš nota falliš f(v°) = sin v° sem stęršfręšilegt bylgjulķkan er aš bylgjur ķ nįttśrunni mišast viš lengd eša tķma en ekki grįšur. Til žess aš bęta śr žessu hefur veriš geršur męlikvarši į horn sem kallast radķanar og byggist į žvķ aš męla lengdir boga eftir einingarhringnum meš einingum hnitakerfisins. Einn radķani samsvarar boga sem er jafn langur og ein eining hnitakerfisins (lengd einnar rśšu).
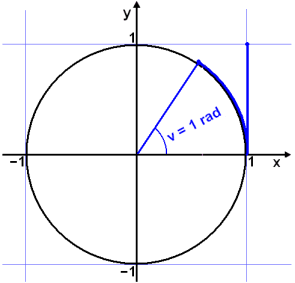
Hugsum okkur aš viš stingjum nišur prjóni śr sveigjanlegu efni viš 1 į x-įs žannig aš prjónshausinn nemi viš hęšina einn į y-įs. Ef viš nś sveigjum prjóninn žannig aš hann leggist aš einingarhringnum žį spannar hann boga sem er ein eining aš lengd og jafn langur radķus hringsins. Mišhorniš sem spannar žennan boga er einn radķani (dregiš af radķus og skammstafaš rad). Žegar horn eru męld į žennan hįtt er talaš um aš nota bogmįl, en ķ raun er veriš aš męla bogan meš radķus einingarhringsins (sem er 1) eša einingum hnitakerfisins.
En hvernig breytum viš grįšum ķ radķana og radķönum ķ grįšur eša grįšum ķ bogmįl og bogmįli ķ grįšur?
Viš getum fundiš žetta samband śt frį žvķ
aš hringur hefur ummįliš 2∙r∙![]() eša 2
eša 2![]() ef męlt
er ķ radķusum. Einingarhringurinn hefur žvķ ummįliš 2
ef męlt
er ķ radķusum. Einingarhringurinn hefur žvķ ummįliš 2![]() ef męlt
er ķ einingum hnitakerfisins. Nišurstašan er eftirfarandi:
ef męlt
er ķ einingum hnitakerfisins. Nišurstašan er eftirfarandi:
2 |
Žegar viš breytum radķönum ķ grįšur margföldum
viš meš hlutfallinu 180/ |
Žegar viš breytum grįšum ķ radķana margföldum
viš meš hlutfallinu
|
Viš skulum nś skoša sķnusbylgjuna ķ
venjulegu hnitakerfi. Til žess žurfum viš aš breyta grįšunum į grafinu ķ
radķana. Žaš gerum viš meš žvķ aš margfalda meš hlutfallinu
![]() /180 og
stytta eins og hęgt er.
/180 og
stytta eins og hęgt er.
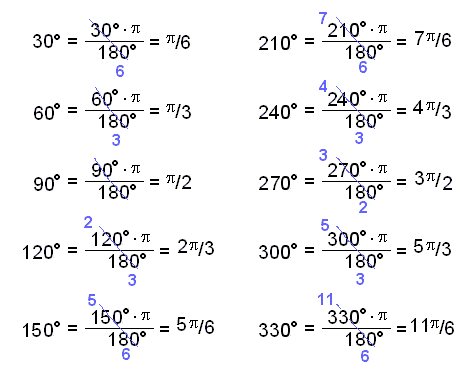
Nś getum viš sett radķanana inn į grafiš og notaš venjulegan x-įs, en viš skulum halda inni grįšunum til samanburšar.
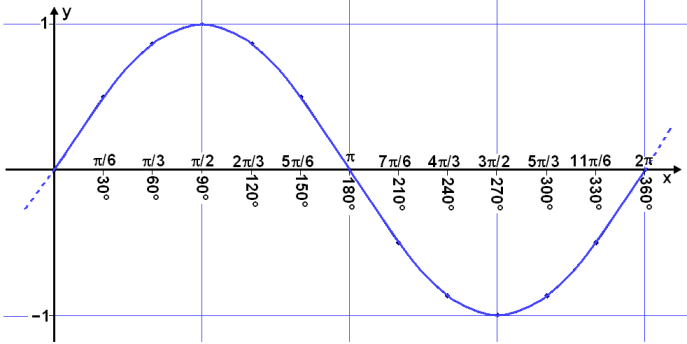
Viš skulum nś reikna śt
hve einn radķani samsvarar mörgum grįšum. Žaš gerum viš meš žvķ aš
margfalda meš hlutfallinu 180/![]() .
.
1∙180°/![]() ≈ 57,3°
≈ 57,3°
Finnum hvaš 5![]() /4 radķanar
samsvara mörgum grįšum. Aftur getum viš margfaldaš meš 180/
/4 radķanar
samsvara mörgum grįšum. Aftur getum viš margfaldaš meš 180/![]() en žaš
er óžarfi vegna žess aš viš vitum aš
en žaš
er óžarfi vegna žess aš viš vitum aš
![]() radķanar
samsvara 180 grįšum. Viš getum žvķ sett 180° inn fyrir
radķanar
samsvara 180 grįšum. Viš getum žvķ sett 180° inn fyrir
![]() .
.
5![]() /4 =
5∙180/4 = 225°.
/4 =
5∙180/4 = 225°.

Ef viš eigum grafķska reiknivél af geršinni CASIO žį er einfalt aš teikna gröf hornafalla, en fyrst veršum viš aš velja hvort viš viljum nota grįšur (e. degrees), radķana (e. radians) eša nżgrįšur (e. grads) en nżgrįšur mišast viš 400 grįšu hring. Raunar žurfum viš aš stilla žetta įšur en viš notum hornaföllin į flestum reiknivélum. Į CASIO-vélum er žetta gert meš žvķ aš velja
Shift og Set Up.
Žį opnast gluggi meš langri röš af stillingarmöguleikum sem viš getum vališ meš fęra okkur upp eša nišur meš örvatökkunum, en nś viljum viš velja horn eša
Angle.
Žį getum viš vališ um eftirfarandi žrjį möguleika:
Deg, Rad, Gra
meš F1, F2 eša F3.
Žar notum viš mest Deg (grįšur) eša Rad (radķana).
Įšur en viš teiknum grafiš veršum viš aš stilla af x-įsinn sem er venjulega nokkuš langur žegar svona bylgjugröf eru teiknuš. Žaš er gert meš žvķ aš velja
Shift og View Window (F3)
Eftir žetta getum viš vališ aš teikna graf.
T.d. grafiš y = sin x

Aš lokum getum viš vališ aš teikna graf meš F6.
Viš skulum nś skoša nokkur gröf ķ töflureikninum EXCEL. Byrjum į žvķ aš teikna grafiš f(x) = cos x. Viš skulum teikna žaš į bilinu −90° til 450° og reikna śt gildin į 30° fresti. Viš byrjum į žvķ aš skrifa −90 efst ķ grįšudįlkinn (ķ B3) og sķšan −60 o.s.frv. (sem er fljótlegast aš afrita).
Excel notar bogmįl žannig aš ķ C-dįlkinn koma tölurnar margfaldašar meš hlutfallinu p/180. Formślan ķ C3 veršur =B3*Pi()/180, en hana mį afrita nišur C-dįlkinn.
Ķ D-dįlkinn kemur sķšan kósķnusfalliš. Formślan ķ D3 veršur =cos(C3) og hana mį afrita nišur.
Grafiš gerum viš sķšan meš žvķ aš blokka B- og D-dįlkana, velja grafstikuna og XY (scatter) og laga grafiš til eftir žörfum. Žaš er einfaldast aš gera meš žvķ aš hęgrismella į žaš sem viš viljum laga. Exceltaflan veršur eftirfarandi:
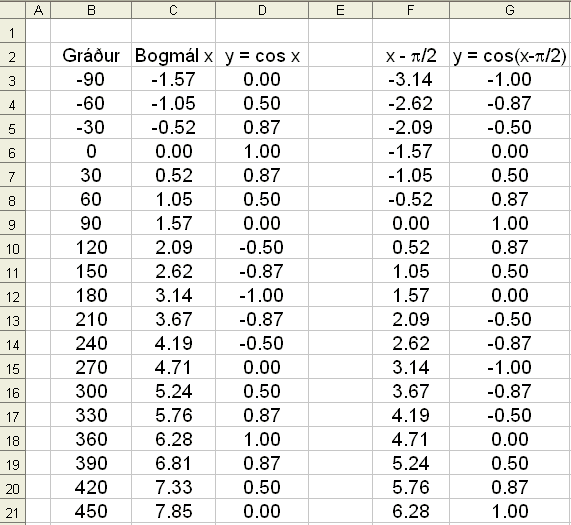
Grafiš y = cos x veršur eftirfarandi:
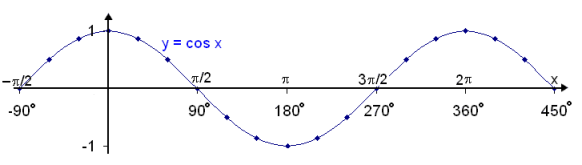
Viš sjįum aš graf kósķnusfallsins
er nįkvęmlega eins og graf sķnusfallsins nema aš sķnusfalliš er hlišraš
sem nemur
![]() /2 (90°) til hęgri.
/2 (90°) til hęgri.
Viš skulum nś prófa aš
draga
![]() /2 frį öllum gildunum ķ C-dįlknum ķ Exceltöflunni og reikna kósķnus
af žvķ
/2 frį öllum gildunum ķ C-dįlknum ķ Exceltöflunni og reikna kósķnus
af žvķ
(sjį F- og G-dįlkana) og teikna upp graf fallsins y = cos(x −
![]() /2).
/2).
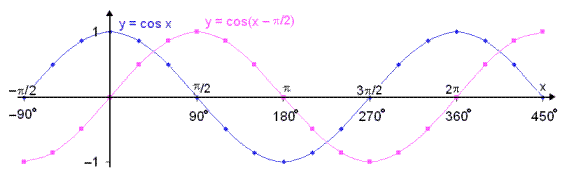
Viš sjįum aš meš žessu höfum viš hlišraš
kósķnusgrafinu
![]() /2 (90°) til hęgri og viš höfum fengiš śt graf sķnusfallsins. Viš
sjįum aš eftirfarandi regla hlżtur aš gilda:
/2 (90°) til hęgri og viš höfum fengiš śt graf sķnusfallsins. Viš
sjįum aš eftirfarandi regla hlżtur aš gilda:
sin x = cos(x −
![]() /2)
/2)
Ennfremur gildir eftirfarandi:
Viš getum hlišraš gröfum hornafallanna til hęgri meš žvķ aš draga fastar stęršir frį breytunni x.
Gröfin y = sin(x − a) og y = cos(x − a) eru gröf sķnus- og kósķnusfallanna hlišruš um a einingar til hęgri ef a > 0 og um a einingar til vinstri ef a < 0. |
Ef a er neikvęš tala žį veršur mķnusinn tvöfaldur žannig aš viš bętum viš x-gildin. Žaš samsvarar hlišrun til vinstri. Viš getum einnig sagt aš grafiš y = cos(x + b) er graf kósķnusfallsins hlišraš um b einingar til vinstri.
Viš skulum nś skoša ķ töflureikni hvaša įhrif margföldun meš tölustušlum hefur į graf sķnusfallsins.
Gröfin verša eftirfarandi:
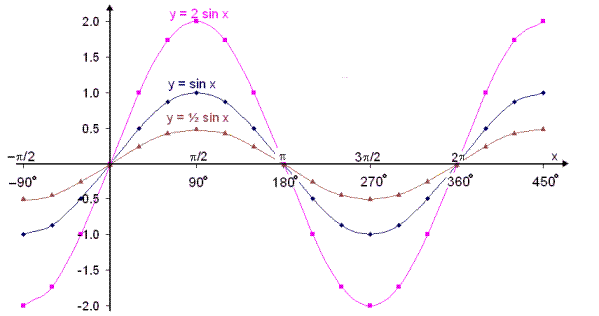
Eins og viš mįtti bśast žį tvöfaldast śtslag bylgjunar ef margfaldaš er meš 2, en śtslag er fjarlęgšin frį mišju bylgjunnar (x-įsnum) upp ķ mestu hęš bylgjunnar. Ef talan sem margfaldaš er meš er minni en einn žį lękkar hins vegar śtslagiš og viš getum einnig slegiš žvķ föstu aš margföldun meš neikvęšri tölu hlżtur aš snśa bylgjunni viš.
Viš skulum nś skoša hvaš gerist ef viš margföldum breytuna x meš fastri stęrš. Berum saman gröfin y = sin x, y = sin 2x og y = sin x/2.
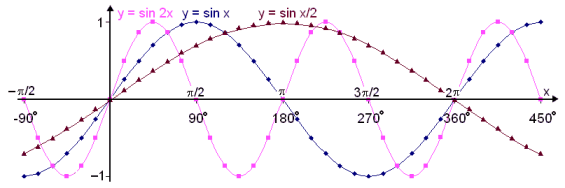
Viš sjįum aš ef viš margföldum breytuna x žį hefur žaš įhrif į bylgjulengd eša lotu fallsins.
Sķnusfalliš hefur
bylgjulengdina eša lotuna 2![]() , en bylgjulengd (eša
lotan) mišast viš žaš bil į x-įsnum sem bylgjan sveiflast frį nślli, upp
ķ hįstöšu, nišur ķ nešstu stöšu og upp ķ nśll aftur.
, en bylgjulengd (eša
lotan) mišast viš žaš bil į x-įsnum sem bylgjan sveiflast frį nślli, upp
ķ hįstöšu, nišur ķ nešstu stöšu og upp ķ nśll aftur.
Bylgjulengd fallsins f(x) =
sin 2x er helmingi styttri en bylgjulengd upprunalegu sķnuskśrfunnar eša
![]() , enda getum viš sagt aš yfirferšin į x-įsnum hafi tvöfaldast.
, enda getum viš sagt aš yfirferšin į x-įsnum hafi tvöfaldast.
Bylgjulengd fallsins f(x) =
sin x/2 er tvöföld mišaš viš bylgjulengd upprunalegu sķnuskśrfunnar eša
4![]() , enda getum viš sagt aš yfirferšin į x-įsnum hafi minnkaš um
helming.
, enda getum viš sagt aš yfirferšin į x-įsnum hafi minnkaš um
helming.
Viš getum sagt aš margföldun
breytunnar meš tölunni b gefur bylgjulengd sem er 2![]() /b.
/b.
Viš getum nś dregiš saman nišurstöšurnar śr sżnidęmunum hér fyrir ofan į eftirfarandi hįtt:
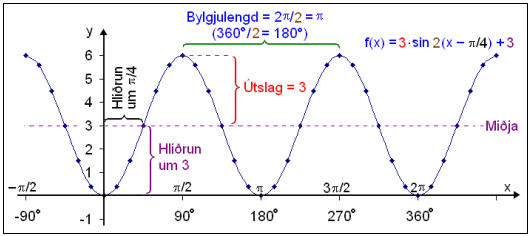
Um falliš f(x) = c∙sin b∙(x − a) + e gildir eftirfarandi: Hlišrun til hęgri er a eininngar (til vinstri ef a er neikvętt). Bylgjulengdin er 2 Śtslagiš er c. Lóšrétt hlišrun į bylgjunni er e (upp ef e > 0, nišur ef e < 0). |
Skošum nś falliš f(x) =
3∙sin 2(x −
![]() /4) + 3
/4) + 3
Falliš ętti aš vera hlišraš
![]() /4 (45°) til hęgri (a =
/4 (45°) til hęgri (a =
![]() /4) og upp um žrjį (e = 3). Śtslagiš ętti aš vera 3 og
bylgjulengdin 2
/4) og upp um žrjį (e = 3). Śtslagiš ętti aš vera 3 og
bylgjulengdin 2![]() /2 =
/2 =
![]() . Viš skulum teikna žetta
upp.
. Viš skulum teikna žetta
upp.
Viš skulum nś skoša graf fallsins f(x) = tan x.
Nś er tan x = sin x/cos x
žanniš aš falliš hlżtur aš hafa lóšréttar ašfellur žar sem cos x veršur
0, en žaš gerist ķ
![]() /2 (90°), 3
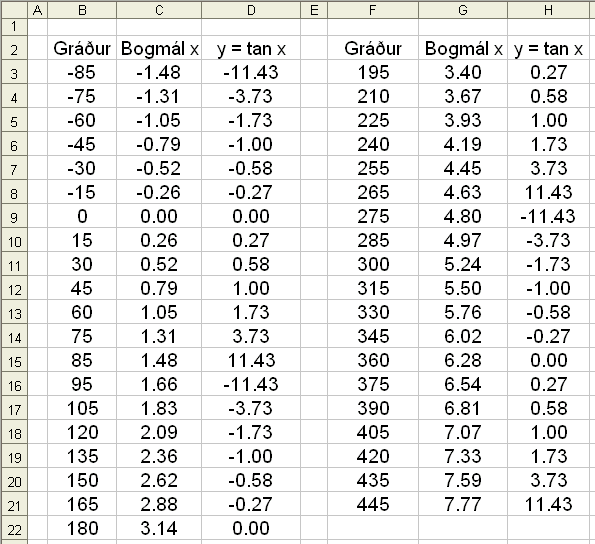
/2 (90°), 3![]() /2 o.s.frv. meš p eininga (180°) millibili. Viš
skulum reikna śt gildistöflu, t.d. ķ töflureikni, en viš getum ekki reiknaš
śt gildi fyrir x-gildin žar sem lóšfellurnar eru.
/2 o.s.frv. meš p eininga (180°) millibili. Viš
skulum reikna śt gildistöflu, t.d. ķ töflureikni, en viš getum ekki reiknaš
śt gildi fyrir x-gildin žar sem lóšfellurnar eru.
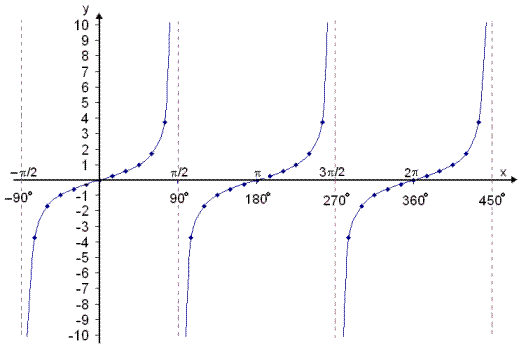
Tangensfalliš er alltaf
vaxandi (stefnir upp). Žaš rķs hratt upp meš ašfellu ķ x = −![]() /2 (−90°). Falliš er
−1 ķ x = −
/2 (−90°). Falliš er
−1 ķ x = −![]() /4 (−45°) og 0 ķ x =
0. Sķšan nęr žaš 1 ķ x =
/4 (−45°) og 0 ķ x =
0. Sķšan nęr žaš 1 ķ x =
![]() /4 (45°) og rķs žašan hratt upp meš ašfellu ķ x =
/4 (45°) og rķs žašan hratt upp meš ašfellu ķ x =
![]() /2 (90°). Žetta endurtekur
sig aftur og aftur og lotan er
/2 (90°). Žetta endurtekur
sig aftur og aftur og lotan er
![]() eša 180°.
eša 180°.
Ęfšu žig į žessum ašferšum og taktu sķšan próf
3 ķ hornaföllum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum