© 2008  Rasmus ehf    og Jóhann Ísak Pétursson

Mengi og Vennmyndir

Kynning 1

Stök hlutmengi

Mengi er vel skilgreint safn talna eða hugtaka.

Einstakir hlutar mengisins kallast hlutmengi.

Stakir einstaklingar, hlutir, tákn eða því um líkt innan mengisins nefnast stök.

Sýnidæmi 1 

Leikmenn íslenska landsliðsins í fótbolta eru gott dæmi um mengi. Eiður væri þá stak í menginu ef átt er við karlalandsliðið en Margrét Lára væri stak í menginu kvennalandslið Íslands.

Tvö tákn eru notuð til þess að segja hvort stak er í tilteknu mengi eða ekki.

             táknar er stak í                 táknar er ekki stak í

Sýnidæmi 2 

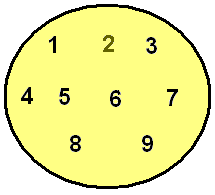
Skoðum mynd af mengi heilla talna á bilinu 1 til 9.

                                   Mengið A

2 er stak í menginu A er táknað 2 A

11 er ekki stak í menginu A er táknað 11 A

Slaufusvigarnir { og } eru oft notaðir til þess að afmarka mengi. Innan þeirra eru þá stökin talin upp eða skilgreind með orðum, mengjatáknum eða ójöfnumerkjum.

   Táknið | inni í mengjasviga merkir þannig að eða þar sem gildir.

   1 x 9 merkir að x er á bilinu 1 til 9 (1 og 9 talin með).

   1 < x < 9 merkir að x er á bilinu 1 til 9 (1 og 9 ekki talin með).

Mengi án staka kallast tómamengi. Það er táknað Ø eða { }.

Sýnidæmi 3

Táknum mengið A í sýnidæmi 2 með mengjasvigum.

   A = {1, 2, 3, 4, 5, 6, 7, 8, 9}

eða

   A = {x | x er heil tala og 1 x 9 }

Mengið hér fyrir neðan sýnir hlutmengi.

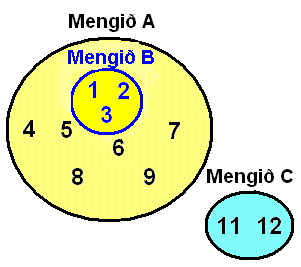Mengið A = {1, 2, 3, 4, 5, 6, 7, 8, 9} Mengið B = {1, 2, 3} Mengið C = {11, 12} Mengið B er hlutmengi í menginu A ef sérhvert stak í B er einnig stak í A.   Mengið C er ekki hlutmengi í A.

Að B er hlutmengi í A er táknað  .

Að C er ekki hlutmengi í A er táknað

Ef til er stak í A sem ekki er í B er mengið B sagt vera eiginlegt hlutmengi  í A. Hér eru stökin 4, 5, 6, 7, 8 og 9 í A en utan við B þannig að B er eiginlegt hlutmengi í A. Ef mengin A og B innihalda sömu stök (A = B) þá er B ekki eiginlegt hlutmengi (en hlutmengi þó).

Að B er eiginlegt hlutmengi í A er táknað .

Reglur:

Sýnidæmi 4

Finnum fjölda hlutmengja í mengjunum A = { }, B = {a}, C = {a, b} og D = { a, b, c}.

A = { }              Ø er eina hlutmengið.

B = {a}             Ø og {a}          2 hlutmengi.

C = {a, b}         Ø, {a}, {b} og {a,b}     4 hlutmengi.

D = {a, b, c}    Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c} og {a,b,c}     8 hlutmengi.

Skoðum fjölda hlutmengja nánar:

Hér er auðsjáanlega ákveðin regla á ferð.

Taktu einnig eftir að röð skiptir ekki máli. T.d. gildir eftirfarandi:

       A            B                  C

   {a,b,c} = {b,a,c} = {a,a,a,b,b,c,c,c,c}   

Röð skiptir ekki máli og ekki skiptir máli þó að sömu stök séu endurtekin.

A = B = C eru jöfn ef þau innihalda sömu stök óháð röð og því hve oft þau koma fyrir.

Sýnidæmi 5

Enska stafrófið er mengi 26 ólíkra stafa. Hve mörg mismunandi hlutmengi eru til af enska stafrófinu?

Samkvæmt reglunni er fjöldi hlutmengja 2²⁶ = 67.108.864