© 2007 Rasmus ehf og Jóhann Ísak
© 2007 Rasmus ehf og Jóhann Ísak |
Şríhyrningar |
|
Hefğ er fyrir şví ağ auğkenna horn í şríhyrningum meğ stórum bókstöfum og hliğar meğ litlum bókstöfum.
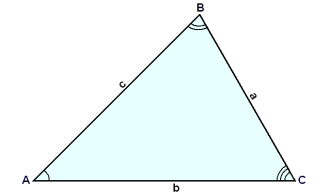
Einnig er hefğ fyrir şví ağ auğkenna mótlægu hliğina á móti horninu A meğ (litlu) a. Einnig er hliğin b mótlæg viğ horniğ B og hliğin c mótlæg viğ horniğ C (sjá mynd). Hliğarnar b og c sem liggja ağ horninu A eru nefndar ağlægar hliğar hornsins A. Hliğin b eğa einhver önnur hliğ sem şríhyrningurinn stendur á er nefnd grunnlína.
Summa allra hornanna í şríhyrningi er 180°. Şağ getum viğ séğ meğ şví ağ teikna línu samsíğa grunnlínunni b í gegnum hornpunktinn B (sjá mynd).
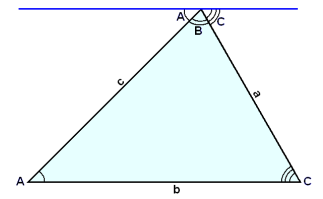
Hornin viğ samsíğa línuna eru A, B og C (sbr. regluna um einslæg horn viğ samsíğa línur) og viğ sjáum ağ A + B + C = 180° vegna şess ağ şau mynda beina línu eğa beint horn eins og şağ er stundum kallağ.
Ef viğ drögum strik frá horninu B beint niğur á grunnlínuna b şannig ağ şağ myndi rétt horn (90°) viğ hana şá nefnist strikiğ hæğ şríhyrningsins.
Şağ er táknağ meğ h á eftirfarandi mynd.
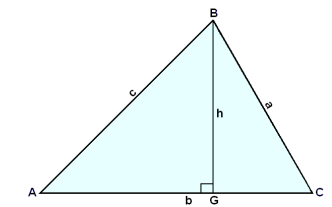
Eins og viğ vitum şá er flatarmál şríhyrnings hálf grunnlínan sinnum hæğin.
F = ½∙b∙h
Hæğin mætir grunnlínunni í punktinum G. Punkturinn G er stundum nefndur fótpunktur hæğarinnar og einnig er talağ um ofanvarp punktsins B á grunnlínuna b (og átt viğ færslu beint niğur eğa hornrétt niğur á b).
Şríhyrningar eru sagğir einslaga ef öll şrjú hornin eru jafn stór. Raunar dugar okkur ağ vita ağ tvö horn eru jafn stór, şar meğ hljóta öll ağ vera jafn stór.
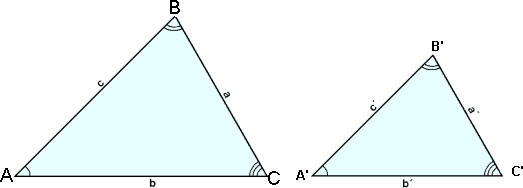
Şríhyrningarnir hér fyrir ofan eru einslaga og şá gildir ağ hlutföll samsvarandi hliğa eru şau sömu. Eftirfarandi gildir:
| og |
Viğ skulum nú ağeins líta á hvernig şessi hlutföll eru notuğ.
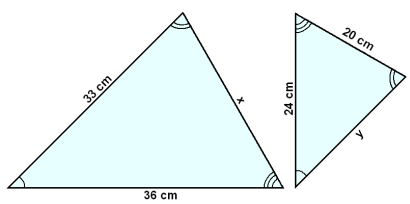
Şríhyrningarnir á myndinni eru einslaga og jafn stór horn eru merkt eins. Finnum hliğarnar x og y.
Viğ skulum byrja á şví ağ merkja hliğarnar meğ sambærilegum táknum til ağ ruglast ekki á hlutföllunum.
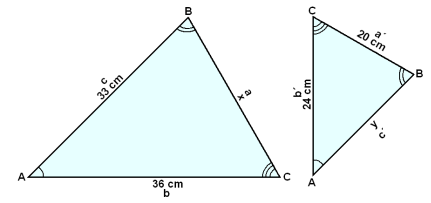
Nú sjáum viğ eftirfarandi hlutföll:
b/c = 36/33 = 24/y = b´/c´
Şá er y/24 = 33/36 og y = 24∙33/36 = 22 cm.
a/b = x/36 = 20/24 = a´/b´
Şá er x = 36∙20/24 = 30 cm.
Svokölluğ rimaregla er afbrigği af hlutföllum einslaga şríhyrninga.
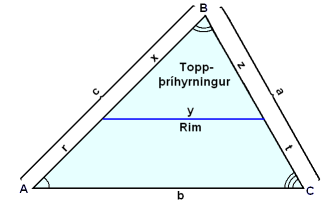 |
|
Rimin skiptir hliğinni c í hlutana x og r og hliğinni a í hlutana z og t. Vegna şess ağ viğ höfum einslaga şríhyrninga şá getum viğ gert eftirfarandi útreikninga:
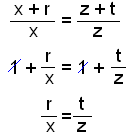
Şetta sınir ağ rimin skiptir hliğum şríhyrningsins í sömu hlutföllum.
Şríhyrningurinn ABC hefur tvær hliğar sem eru 30 cm langar og 42 cm grunnlínu. Dregin er rim sem er 14 cm löng samsíğa grunnlínunni. Finnum hvernig rimin skiptir 30 cm hliğunum (finnum XB og Ax).
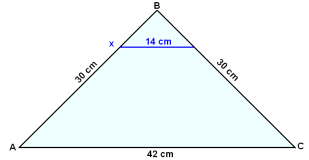
14/42 = XB/30
XB = 30∙14/42 = 10 cm
AX = 30 − 10 = 20 cm
Um stærğir horna í şríhyrningum er lítiğ hægt ağ vita nema meğ mælingum og útreikningum (meğ hornaföllum). Şó eru şar á nokkrar gagnlegar undantekningar.
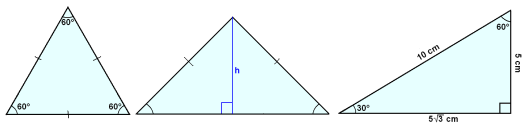
Jafnhliğa şríh. Jafnarma şríh. Rétthyrndur şríh.
Jafnhliğa şríhyrningur hefur allar hliğar jafn langar (merkt meğ striki) og öll hornin 60°.
Jafnarma şríhyrningur hefur tvær jafn langar hliğar og tvö jafn stór horn viğ grunnlínuna (sem ekki er jafn löng og hinar tvær). Viğ şurfum şví ekki ağ vita nema eitt horn til şess ağ finna hin. Ef viğ drögum hæğ á grunnlínuna şá skiptum viğ jafnarma og jafnhliğa şríhyrningum í tvo jafn stóra rétthyrnda şríhyrninga.
Ef lengdir hliğa í şríhyrningi uppfylla skilyrğin sem Pışagórasarreglan setur (a2 + b2 = c2) şá er hann rétthyrndur. Reglan gildir sem sagt í báğar áttir. Hún gildir fyrir şríhyrninginn lengst til hægri á myndinni hér fyrir ofan eins og sést á eftirfarandi útreikningum:
52 + (5![]() )2 = 102
)2 = 102
25 + 75 = 100
Hér stendur şannig á ağ şríhyrningurinn á myndinni hefur langhliğ (10 cm) sem er tvöföld styttri skammhliğin (5 cm). Í öllum slíkum şríhyrningum eru hornin 30°, 60°og 90°.
Finnum flatarmál şríhyrnings sem hefur allar hliğar jafn langar eğa 10 cm.
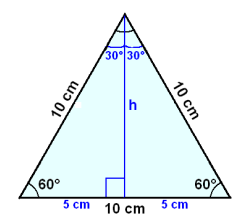
Viğ byrjum á şví ağ draga hæğ á eina hliğina. Meğ şví skiptum viğ henni í tvo 5 cm búta. Şar meğ höfum viğ tvo rétthyrnda şríhyrninga og getum notağ Pışagórasarregluna til şess ağ reikna hæğina.
h2 + 52 = 102
h2 = 102 − 52 = 100 − 25 = 75 = 52∙3
h = 5![]() ≈ 8,7
≈ 8,7
F = ½∙10∙h ≈ ½∙10∙8,7 ≈ 43 cm2
Şríhyrningur hefur tvær hliğar 30 cm langar og 42 cm langa grunnlínu. Teiknuğ er rim í 10 cm fjarlægğ frá grunnlínunni. Finnum hve löng rimin er.
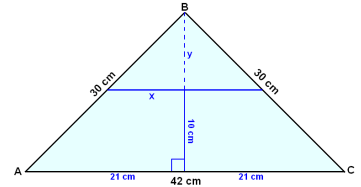
Viğ byrjum á şví ağ draga hæğ á grunnlínuna. Şar meğ höfum fengiğ tvo rétthyrnda şríhyrninga og getum şá notağ Pışagorasarreglu. Reiknum hæğina.
h2 + 212 = 302
h2 = 302 − 212 = 459
h ≈ 21,4
Nú er y = h − 10 ≈ 21,4 − 10 ≈ 11,4 cm
Síğan notum viğ okkur ağ şríhyrningarnir eru einslaga.
y/h = x/ 21
x ≈ 21∙11,4/ 21,4 ≈ 11 cm
Şetta segir okkur ağ rimin er nálægt şví ağ vera 22 cm löng.
Viğ skulum stilla rétthyrndum şríhyrningi şannig upp ağ langhliğin verği grunnlína, en şá myndar 90° horniğ toppinn. Drögum síğan hæğ eins og eftirfarandi myndi sınir:
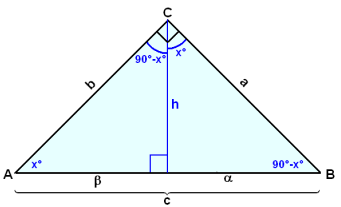
Hæğin skiptir 90° horninu í tvennt. Viğ skulum kalla annan hlutann x°, en hinn hlutinn verğur şá 90°− x°. Viğ sjáum şá ağ hornin viğ grunnlínuna sitt hvoru megin verğa ağ vera 90° − x° hægra megin og x° vinstra megin ef şríhyrningarnir eiga ağ hafa samtals 180° hornasummu.
Nú sjáum viğ ağ stóri şríhyrningurinn og báğir litlu şríhyrningarnir hafa 90°, x° og 90° − x° horn. Şeir hafa allir jafn stór horn og eru şví einslaga.
Fyrir alla rétthyrnda şríhyrninga gildir ağ hæğ á langhliğina skiptir şeim í tvo şríhyrninga sem eru báğir einslaga upprunalega şríhyrningnum.
Şetta gefur möguleika á şrenns konar hlutföllum.
Hlutföllin mótlægar hliğar viğ horniğ x° deilt meğ mótlægum hliğum viğ 90°− x° eru eftirfarandi:
![]()
Hlutföllin mótlægar hliğar viğ horniğ x° deilt meğ langhliğum eru eftirfarandi:
![]()
Hlutföllin mótlægar hliğar viğ horniğ 90° − x° deilt meğ langhliğum eru eftirfarandi:
![]()
Rétthyrndur şríhyrningur hefur skammhliğarnar 7 cm og 10 cm. Dregin er hæğ á grunnlínuna. Finnum flatarmál şríhyrninganna tveggja sem myndast.
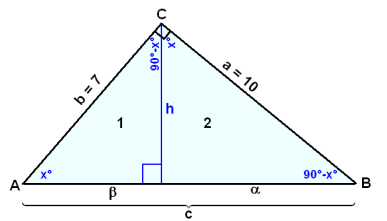
Viğ byrjum á şví ağ reikna út hliğina c meğ Pışagórasarreglu.
c2 = 102 + 72 = 149, şá er c ≈ 12,2 cm
Reiknum næst a.
a/c = a/a
a = a2/c ≈ 102/12,2 ≈ 8,2 cm
Og síğan b.
b ≈ 12,2 − 8,2 ≈ 4 cm
Şá vantar okkur h til şess ağ finna flatarmálin.
b/c = h/a
h = ab/c ≈ 10∙7/12,2 ≈ 5,7 cm
Nú getum viğ reiknağ flatarmálin.
F1 = ½∙b∙h ≈ ½∙4∙5,7 ≈ 11,4 cm2
F2 = ½∙a∙h ≈ ½∙8,2∙5,7 ≈ 23,4 cm2
Æfğu şig á şessum ağferğum og taktu síğan próf
1 í şríhyrningum.
ps. mundu eftir ağ fylla út í tékklistann şinn jafnóğum