© 2008 Rasmus ehf og Jóhann Ķsak
|
© 2008 Rasmus ehf og Jóhann Ķsak |
Afleišu
|
|
Rętur, neikvęš veldi, margfeldi og ręš föll
Finnum afleišu ![]() .
.
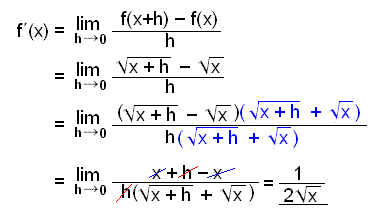 |
Viš notum okkur samokaregluna a2b2 = (ab)(a+b) til žess aš breyta stęšunni og stytta h-iš śr nefnaranum. |
Athugum nś hvort viš fįum žaš sama śt ef
viš skrifum kvašratrótina sem hįlfta veldi (![]() )
og notum regluna
)
og notum regluna ![]() .
.
![]()
|
Viš getum notaš regluna: f“(x) = n·x n1 į rótarvķsa. |
Finnum afleišu fallsins .
Viš
byrjum į žvķ aš einfalda stęšuna og skrifa sem eitt veldi og rifjum upp
regluna ![]() žar sem
n
er rótarvķsir og v veldisvķsir sem verša nefnari og teljari ķ veldisvķsi
sem er brot.
žar sem
n
er rótarvķsir og v veldisvķsir sem verša nefnari og teljari ķ veldisvķsi
sem er brot.
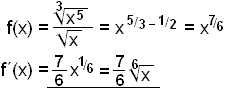 |
Viš fęrum 7/6 framfyrir og lękkum veldisvķsinn um 1. |
Finnum nś afleišu fallsins f(x) = x1 = 1/x.
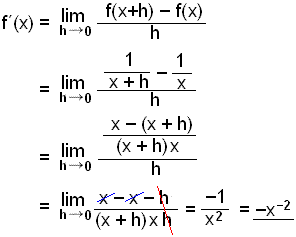 |
Viš setjum fyrst upp į strik fyrir ofan ašalstrikiš og setjum sķšan nišur į eitt strik. Aš lokum styttum viš og einföldum. |
|
Viš getum notaš regluna f“(x) = n·x n1 į neikvęša veldisvķsa |
Finnum afleišu margfeldis tveggja falla.
f(x) = u(x)·v(x).
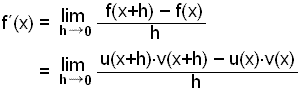
Nś er mašalvaxtarhraši falla į žröngu bili nįlęgt žvķ aš vera jafn afleišunni žannig aš eftirfarandi gildir um u“(x) og v“(x).
![]() og
og
![]()
Śt frį žessu fįum viš
h·u“(x) » u(x+h) u(x) žannig aš u(x+h) » h·u“(x) + u(x)
h·v“(x) » v(x+h) v(x) žannig aš v(x+h) » h·v“(x) + v(x)
Žessar stęšur getum viš sett inn ķ markgildiš hér fyrir ofan og einfaldaš vegna žess aš nįlgunin veršur nįkvęmari eftir žvķ sem x minnkar. Ef viš einföldum og reiknum markgildiš į žennan hįtt žį fįum viš eftirfarandi reglu fyrir afleišu margfeldis tveggja falla:
|
(u(x)·v(x))“= u“(x)·v(x) + u(x)·v“(x) |
Žessa reglu getum viš sett upp į einfaldari hįtt sem žęgilegra er aš muna en viš veršum aš hafa ķ huga aš u og v eru föll.
|
(uv)“ = u“v + uv“ |
Nś getum viš aš sjįlfsögšu margfalda saman og fengiš śt f(x) = x5 og f“(x) = 5x4, en viš skulum nota regluna hér fyrir ofan.
Setjum u = x3 sem gefur u“ = 3x2 og v = x2 sem gefur v“ = 2x.
f“(x) = (uv)“ = u“v + uv“
= 3x2·x2 + x3·2x
= 3x4 + 2x4 = 5x4
Finnum afleišu hlutfallsins u/v žar sem u og v eru föll:
![]()
Nś er (v1)“ = v2·v“ samkvęmt reglunni um afleišu veldastęrša og kešjureglunni sem sżnd er ķ kynningu 5. Viš getum žvķ leyst žetta meš reglunni (uv)“ = u“v + uv“.
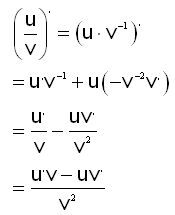
Regla til žess aš finna afleišu hlutfalls tveggja falla er eftirfarandi:
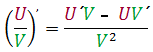 |
Finnum afleišu ![]()
Setjum u = x + 1 sem gefur u“ = 1 og v = x2 sem gefur v“ = 2x.
Röšum žessu nś inn ķ regluna hér fyrir ofan.
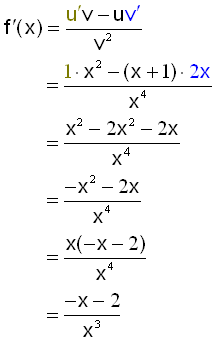
Ęfšu žig į žessum ašferšum og taktu sķšan próf
3 ķ afleišum.
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum