© 2000 - 2010 Rasmus ehf

Hnitakerfið og jöfnur

Kynning 1.

Jafna beinnar línu.

Jöfnur á forminu y = ax + b , þar sem a og b eru þekktar stærðir, eru jöfnur fyrir beina línu.  Það þarf að þekkja minnst tvo punkta á einhverri línu svo að hægt sé að teikna hana. Skynsamlegt er samt að reikna alltaf út minnst 3 punkta á línu.

Gildistafla:  Þegar jafna einhverrar línu er þekkt er gott að gera sér töflu yfir þau gildi sem við reiknum út, það er kallað gildistafla. 

Tökum sem dæmi línuna:  y = x + 1

Þetta samband á milli breytistærðanna verður alltaf að standast, en þú hefur leyfi til að velja hvað sem þú villt í staðinn fyrir x og reiknar síðan út hvaða gildi passa fyrir y.

Gildistafla fyrir y = x + 1

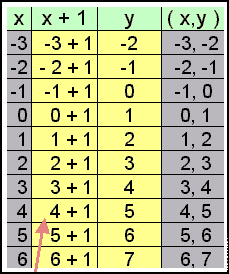
    Ath. þú ræður hve mörg gildi þú nennir að reikna út. En ath. reiknaðu alltaf  lágmark gildi fyrir þrjá punkta. Ef þessir völdu punktar þínir eru ekki svo þægir að vilja vera á sömu línunni, þá hefur þú reiknað rangt og verður að endurskoða útreikninginn.

 Graf sem sýnir mynd af línunni: y = x + 1

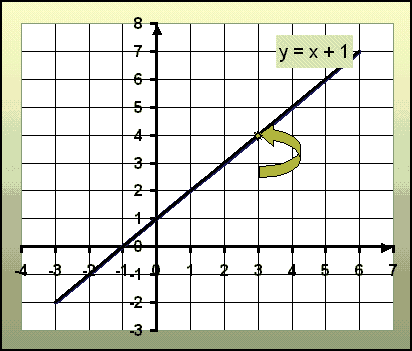
    Við sjáum píluna sem bendir á punktinn (3,4) en það er dæmi um einn punkt sem fenginn er úr gildistöflunni, annar punktur er t.d. (0,1) sem er einmitt punkturinn þar sem línan keyrir í gegnum y ásinn. Með tvo slíka punkta merkta inn í línuritið, er auðvelt að teikna línuna með því að draga strik á milli punktanna.

Fleygbogar

Jöfnur á forminu y = ax² + b  þar sem a og b eru þekktar stærðir, eru jöfnur fyrir fleygboga. Til að teikna graf fyrir slíkar jöfnur þarf að reikna út mun fleiri en þrjá punkta.

Dæmi: gefin er jafnan y = x² - 4

Við reiknum út nokkur gildi fyrir x á bilinu -4 til + 4

þá er að vinda sér í gildistöflu alveg eins og áður.

Gildistafla fyrir  y = x² - 4 

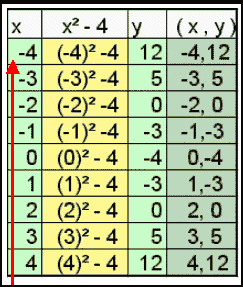
 Dæmi set x = -4 þá er y = (-4)² - 4 = 16 - 4 = 12

Hér sést að sum gildin koma stundum tvisvar fyrir á y, það er vegna þess að fleygbogar eru samhverfir.

Graf sem sýnir mynd af fleygboganum

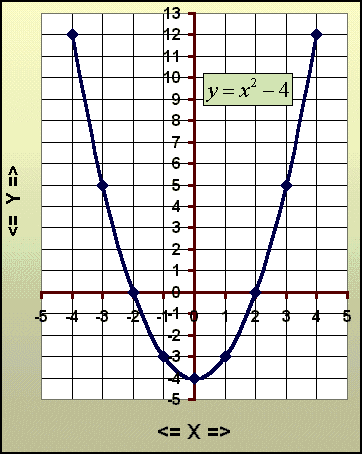Ef við skoðum efstu punktana á myndinni  eða punkt með hnitin (4,12)  þá sést að hann á sér hliðstæðu í punktinum (-4,12)   Taktu vel eftir hvar fleygboginn sker y ás og hvar hann sker x ásinn.

Ef þú þáttar jöfnuna y = x² - 4   Fæst x² - 4 = (x - 2)(x + 2)

ef við setjum y = 0 þá sést að x þarf að verða annað hvort +2 eða - 2 til að jafnan standist. Þá fást hnitin (-2,0) og (+2,0) en það eru einmitt skurðpunktarnir við x ás.

Hallatala beinnar línu:

Skoðum línuna y = 2x + 1

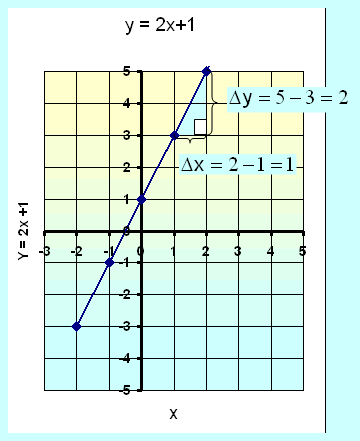Hallatala þessarar línu er 2 sem er stuðullinn við x. Einnig er hægt að reikna hallatöluna út með því að teikna rétthyrndan þríhyrning við hliðina á línunni og reikna breytingu miðað við y ás og deila síðan með breytingunni miðað við x ás. Lóðrétt breyting Δy = 5 -3 = 2 Lárétt breyting Δx = 2 -1 = 1 Hallatala línunnar er þá 2/1 = 2 ( Þegar við ferðumst eftir línunni frá 1,3 til 2,5 þá hækkar gildið á y um 2 en gildið á x um 1 )

Taktu nú próf 1 í Hnitakerfinu.