© 2004  Rasmus ehf

Tölfræði

Kynning 2

    Meðaltal, miðgildi og tíðasta gildi:

Meðaltal

Dæmi 1. 

Skoðum hæð 5 tólf ára nemanda í cm.
Stína er 143cm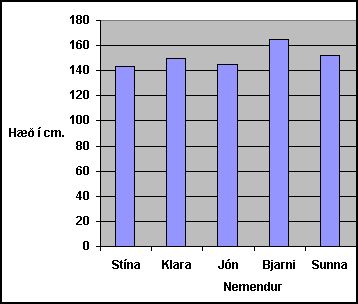
Klara er 150cm,
Jón er 145cm
Bjarni er 165cm
Sunna 152cm

Finnum meðalhæð nemandanna með því að leggja saman hæð þeirra og deila í með fjölda þeirra.    

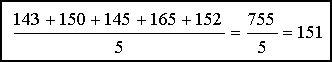    Eða 151cm.

Meðaltalið er 151cm.  (Ath mælingarnar eru í cm.)

Miðgildi

Dæmi 2.  Skoðum meðalhæð hjá öðrum fimm nemendum:

Guðrún 149cm, Páll 192cm, Andrés 151cm, Sif 153cm, Eva 155cm

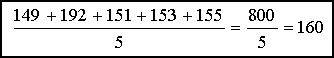    Eða 160cm.

Meðaltalið er 160cm.  (Ath mælingarnar eru í cm.)

Miðgildið er fundið með því að raða tölusafni eftir stærð og finna töluna í miðjunni.

Röðum krökkunum úr dæmi 2 eftir stærð.

  Við sjáum að talan í miðjunni er 153cm.

Þá er miðgildið = 153cm.  (Ath meðaltal er ekki sama fyrirbærið og miðgildi ).

Finnum nú miðgildi fyrir alla nemendur úr dæmum 1 og 2 hér á undan.

Röðum mælingunum í vaxandi röð:  

143cm, 145cm, 149cm, 150cm, 151cm, 152cm, 153cm, 155cm, 165cm, 192cm.

Miðgildið fæst með því að finna meðaltal talnanna sem eru sitthvoru megin við miðjuna.

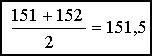
Miðgildið er því 151,5cm.

Þegar engin mæling er í miðjunni, þá leggjum við saman tölurnar sitt hvoru megin við miðjuna og deilum með 2.

Tíðasta gildi

Dæmi 3.

Skoðum súluritið yfir ferðir nemenda í kvikmyndahús úr kynningu 1

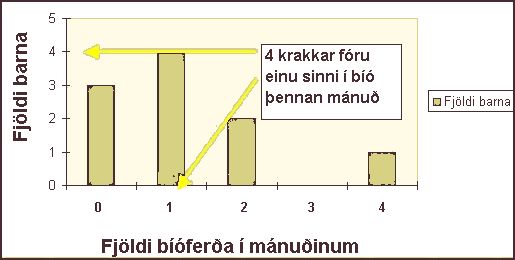
Flestir úr þessum hóp fóru einu sinni á mánuði í bíó eða 4 krakkar.

Tíðasta gildið er því 1.

Tíðasta gildi merkir það gildið sem kemur oftast fyrir.

Æfðu þig á þessum aðferðum og taktu síðan próf 2 í Tölfræði.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum.