© 2007 Rasmus ehf og Jóhann Ķsak
© 2007 Rasmus ehf og Jóhann Ķsak |
Mengi kynning 3 |
|
Viš getum hugsaš okkur talnalķnu sem žétta samfellda röš af punktum. Hver punktur į talnalķnunni tįknar tölu sem samsvarar fjarlęgš hans frį nśllpunktinum til vinstri (−) eša hęgri (+).
Talnamengin Z (heilar tölur) og N (nįttśrulegar tölur) geta ekki einar og sér myndaš talnalķnu, ašeins staka punkta į henni.
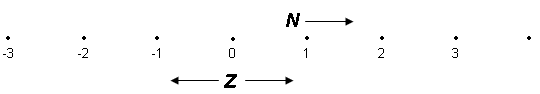
Mengiš Q, mengi ręšra talna, myndar heldur ekki samfellda talnalķnu. Inni į milli ręšu talnanna er óendanlegur fjöldi talna sem ekki er hęgt aš tjį nįkvęmlega meš almennu broti žannig aš mengiš Q er ķ raun slitrótt ef vel er aš gįš.
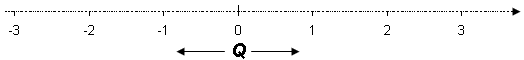
Tölurnar sem vantar uppį heita óręšar tölur. Ef reynt er aš skrifa žęr meš óendanlegum tugabrotum kemur aldrei fram nein endurtekning eša lota. Eftirfarandi eru nokkur dęmi um nįlganir į óręšum tölum:
| 0,909009000900009 |
| 0,123456789101112 |
|
|
|
|
| p = 3,141592653589 |
Óręšu tölurnar įsamt ręšu tölunum eša menginu Q (sem inniheldur mengin Z og N) mynda samfellu sem viš könnumst viš sem talnalķnu eša x-įs. Saman mynda žessi mengi eina heild sem kallast rauntölur eša talnamengiš R.
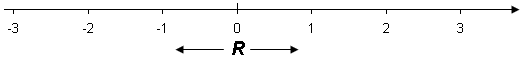
Eftirfarandi mynd sżnir hvernig mengiš R nęr yfir talnamengin Q, Z og N. Žar kemur fram hvernig mengi rauntalna skiptist ķ óręšar tölur (óstrikaš svęši) og brot (mengiš Q). Mengiš Q skiptist sķšan ķ brot og heilar tölur (mengiš Z). Mengiš Z skiptist loks ķ Mengiš Z-, 0 og mengi nįttśrulegra talna (N).
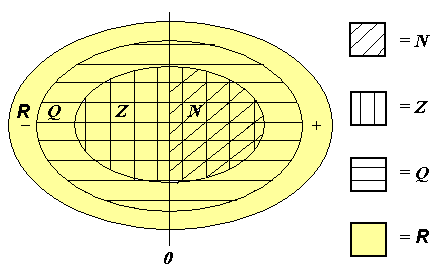
Hęgt er aš tįkna bil į talnalķnu meš żmsu móti. Biliš frį og meš 1 til og meš 5 mį t.d. tįkna į eftirfarandi hįtt:
Meš ójöfnu: 1
![]() x
x
![]() 5
5
Meš mengjatįknum: { x![]() R | 1
R | 1
![]() x
x
![]() 5}
5}
Meš teikningu:
![]()
Einnig er algengt aš tįkna bil meš svoköllušum biltįknum sem eru hornklofar. Biliš frį 1 til 5 meš endapunktunum veršur žį
[1; 5] eša [1, 5] (mismunandi eftir bókum)
Bil eins og [1; 5] žar sem bįšir endapunktarnir eru taldir meš kallast lokaš bil.
Nś er žaš ęši oft žannig aš ekki er unnt aš gefa einhvern fastan įkvešinn punkt sem fyrsta eša sķšasta punkt ķ mengi. Tökum sem dęmi allar tölur stęrri en 1 og minni en 5 (endapunktarnir 1 og 5 er ekki taldir meš). Žetta mį tįkna į żmsa vegu, t.d.:
| Ójafna: | 1 < x < 5 | |
| Mengjatįkn: | { x
|
|
| Teikning: | ||
| Biltįkn: |
|
mismunandi eftir bókum |
Taktu eftir aš nś eru endapunktarnir 1 og 5 hafšir holir hringir į myndinni og opnir hornklofar žegar biltįkn eru notuš.
|
Merkin
|
|
Bil
eins og |
Skošum aš lokum hvernig biliš frį og meš einum og upp śr er tįknaš:
| Ójafna: | x ≥ 1 | |
| Mengjatįkn: | { x
|
|
| Teikning: | ||
| Biltįkn: |
|
mismunandi eftir bókum |
Bil eins og žetta kallast hįlfopiš (eša hįlflokaš). Hįlfopin bil žurfa ekki aš nį upp ķ óendanleikann.
| Biliš |
|
er hįlfopiš. Skošašu myndina af žvķ hér fyrir nešan. |
![]()
Ęfšu žig į žessum ašferšum og taktu sķšan próf
3 ķ Mengjum .
ps. mundu eftir aš fylla śt ķ tékklistann žinn jafnóšum