© 2007 Rasmus ehf og Jóhann Ísak
|
© 2007 Rasmus ehf og Jóhann Ísak |
Afleiğur |
|
Keğjureglan
Ef viğ skoğum falliğ f(g) = g3 şá hefur şağ afleiğuna f´(g) = 3g2. Hvağ gerist nú ef g er fall en ekki venjuleg einföld breyta? Viğ getum t.d. sett g(x) = x2.
Skoğum afleiğuna af samsetta fallinu.
f(x2) = (x2)3 = x6
Hún hlıtur ağ vera 6x5. Skoğum şağ nánar meğ şeim ağferğum sem viğ höfum notağ hingağ til.
f´(x2) = 3(x2)2 = 3x4
Hér vantar ağ margfalda meğ 2x til şess ağ fá afleiğu samsetta fallsins.
(f(g(x))´ = 3(x2)2·2x = 6x5
Nú er afleiğa innra fallsins g(x) = x2 engin önnur en g´(x) = 2x şannig ağ eftirfarandi regla gildir fyrir şessa samsetningu:
|
(f(g(x))´ = f´(g(x))·g´(x) |
Sına má fram á ağ şessi regla gildir fyrir öll samsett föll sem eru samfelld og hafa afleiğu.
Finnum afleiğu samsetta fallsins f(x) = sin2x.
Rithátturinn sin2x hefur sömu merkingu og (sin x)2 şannig ağ annağ veldi er ytra fall en sin x innra. Afleiğan verğur şá
f´(x) = 2(sin x)·cos x = 2 sin x cos x
Afleiğa ytra fallsins er reiknuğ eins og innra falliğ væri venjuleg. Síğan er margfaldağ meğ afleiğu innra fallsins.
Finnum afleiğu f(x) = sin x2.
Hér er sínus ytra fall en annağ veldi innra fall.
f´(x) = cos x2 · 2x
cos x = f(x) = sin (![]() x)
x)
Nú hefur sinusfalliğ afleiğuna cos og (![]()
x) afleiğuna 1 şannig ağ
x) afleiğuna 1 şannig ağ
f´(x)
= cos(![]() x)·(1)
x)·(1)
= sin x · (1)
= sin x
Finnum afleiğu f(x) = sin2x2.
Şetta jafngildir f(x) = (sin x2)2 şannig ağ falliğ er şrefallt, annağ veldi yst, şar næst er sinusfalliğ og innsta falliğ er síğan aftur annağ veldi. Hér sjáum viğ ağ nafn keğjureglunnar er sannkallağ réttnefni.
|
f´(x) = 2 sin x2
· cos x2 · 2x |
Fyrst
kemur afleiğa annars veldis og sin x2
óbreytt. |
|
a)
f(x) = e2x
|
Afleiğa vísisfallsins er falliğ óbreytt, afleiğa 2x er 2. |
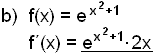 |
Afleiğa vísisfallsins er falliğ óbreytt, afleiğa x2 + 1 er 2x. |
|
c) f(x) = esin
x |
Afleiğa vísisfallsins er falliğ óbreytt, afleiğa sin x er cos x. |
Sýnidæmi 6
Við skulum nú finna afleiðu ax.
f(x) = ax
Rifjum fyrst upp lograregluna ln ax = x·ln a. Ef við setjum báðar hliðar sem veldi á e þá fáum við eftirfarandi framsettningu á fallinu f(x) = ax.
f(x) = ax = ex·ln a
Nú er ln a fasti eins og hvert annað k þannig að við getum fundið afleiðu ax ef við umritum það á formið ex·ln a.
f´(x) = (ex·ln a)´ = (ln a)·ex·ln a = (ln a)·ax
Fallið f(x) = ax hefur afleiðuna (ln a)·ax |
Finnum afleiðu fallsins f(x) = ex·ax.
Hér notum við regluna (uv)´= u´v + uv´ þar sem u = ex sem gefur u´ = ex og v = ax sem gefur v´ = (ln a)·ax. Röðum þessu nú inn í regluna.
f´(x) = (uv)´= u´v + uv´
= ex·ax + ex·(ln a)·ax Hér tökum við exax út fyrir sviga.
= exax(1 + ln a)
Sýnidæmi 8
Finnum afleiğu náttúrulega lografallsins f(x) = ln x.
Ef f(x) = ln x şá er ef(x) = x. Ef viğ nú finnum afleiğu beggja hliğa jöfnunnar şá fáum viğ eftirfarandi:
ef(x) = x
ef(x)·f´(x) = 1 Hér notum viğ keğjuregluna.
Leysum nú fyrir f´(x).
f´(x) = 1/ef(x)
= 1/x Munum ağ x = e f(x).
Í framhaldinu getum viğ fundiğ afleiğur annarra lografalla.
Finnum afleiğu f(x) = log x.
Nú şurfum viğ ağ dusta rykiğ af reglu sem sındi tengsl logra meğ mismunandi grunntölu a. Reglan var eftirfarandi:
![]()
Viğ getum notağ şessa reglu til şess ağ umrita ağra logra yfir á náttúrulega logran ln x.
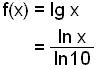
Logrinn ln 10 er fasti sem breytir engu şannig ağ eftirleikurinn er auğveldur.
![]()
Sambærileg útreikninga má gera fyrir ağra logra şannig ağ eftirfarandi şrjár reglur gilda fyrir afleiğur lografalla:
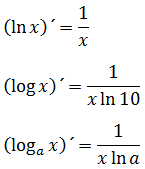 |
Finnum afleiğu f(x) = ln(x2 + 1).
Finnum afleiğu f(x) = x·ln x x + 5.
f´(x) = 1·lnx + x·1/x 1 = ln x
Afleiğur:
k´ = 0 k = fasti
x´ = 1
(xn)´ = nxn1 n getur m.a. veriğ neikvæğ tala eğa brot
(ex)´ = ex
(ax)´ = ax · ln a
sin´x = cos x
cos´x = sin x
![]()
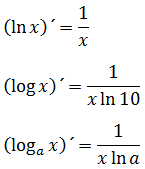
(uv)´ = u´v + uv´
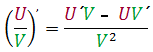
(f(g(x))´ = f´(g(x))·g´(x)
Æfğu şig á şessum ağferğum og taktu síğan próf
5 í afleiğum.
ps. mundu eftir ağ fylla út í tékklistann şinn jafnóğum