© 2008  Rasmus ehf    og Jóhann Ísak

Heildun

Kynning 1

Stofnföll

Við höfum kynnst því fyrr hvernig finna má afleiður og hvernig finna má halla snertils við gröf falla. Slíkur reikningur kallast einu nafni deildun (eða diffrun).

Andhverfa deildunnar nefnist heildun og helsta aðgerðin í heildun er að finna fall út frá afleiðu þess.

Ef við þurfum að finna fallið F(x) og vitum að afleiða þess er annað fall f(x) þá er F(x) kallað stofnfall f(x).  Hefð er fyrir því að auðkenna stofnföll með stórum staf.

Sýnidæmi 1

Flugeldi er skotið af skipi beint upp í loftið. Hann nær 130 m hæð áður en hann stöðvast í eitt augnablik og tekur að falla til jarðar. Mælingar frá landi sýna að hraði flugeldsins fylgir nokkurn veginn jöfnunni f(t) = 50 – 10t ef t táknar tímann í sekúndum. Finnum fall sem sýnir hæð flugeldsins á hverjum tíma.

Í umfjöllun um deildun kynntumst við því hvernig afleiða staðsetningarfalls gaf okkur hraðafall. Nú þurfum við að finna staðsetningarfall (hæðarfall) út frá hraðafalli. Við þurfum að finna stofnfallið F(t) sem er þannig að F´(t) = 50 – 10t = f(t).

Við vitum að 50t verður 50 í deildun (t´ = 1). Einnig vitum við að deildun lækkar veldisvísi um einn og síðan er margfaldað með gamla veldisvísinum. Andhverf aðgerð hlýtur þá að vera að hækka veldisvísinn um einn og deila síðan með veldisvísinum sem kemur út til þess að upphefja margföldunina. Þetta gefur okkur eftirfarandi stofnfall:

   F(t) = 50t –10t²/2 = 50t – 5t²

Við fallið f(t) má bæta núlli. Það merkir að við stofnfallið getur bæst hvaða tala C sem er vegna þess að afleiða tölu er núll (C´ = 0). Endanlegt stofnfall verður því F(t) = 50t – 5t² + C. Fastinn C segir til um hvar graf F(t) sker y-ásinn. Til þess að reikna hann verðum við að vita einhvern fastann punkt á grafinu. Og við vitum að topppunkturinn er í 130 m hæð sem gefur okkur fastan punkt til að reikna út C.

   F´(t) = 50 – 10t = 0

                      10t = 50

                          t = 5

Topppunkturinn er (5, 130) sem segir okkur að eftir 5 s hefur flugeldurin náð mestri hæð sem er 130 m.

   F(5) = 50·5 – 5·5² + C = 130

               250 – 125 + C = 130

                                    C = 130 – 125 = 5

Þetta bendir til þess að flugeldinum hafi verið skotið úr 5 m hæð. Fall sem sýnir hæð flugeldsins á hverjum tíma er þá

   F(t) = 50t – 5t² + 5

Sýnidæmi 2

Athugum nú hvernig við getum fundið stofnfall margliða.

1)   Skoðum fyrst f(x) = x.

      Stofnfallið hlýtur að vera í öðru veldi vegna þess að deildun lækkar veldið um einn. Andhverf aðgerð hlýtur þá að hækka veldið um einn. Við verðum einnig að deila
      með veldisvísinum 2 vegna þess að í deildun er margfaldað með 2. Við verðum einnig að bæta við föstu stærðinni C sem við vitum ekki hver er vegna þess að
      slíkar stærðir verða 0 í deildun.

           F(x) = x²/2 + C

      Prófum nú þessa niðurstöðu með deildun.

         F´(x) = f(x) = 2x/2 + 0 = x

      Þetta passar.

2)   Finnum stofnfall f(x) = x³.

      Hækkum veldið upp í fjóra, deilum með 4 og bætum við fastanum C.

         F(x) = x⁴/4 + C

      Prófum þessa niðurstöðu.

         F´(x) = f(x) = 4x³/4 + 0 = x³

      Þetta passar.

3)   Finnum stofnfall f(x) = xⁿ.

      Hækkum veldið upp um einn, deilum með hækkaða veldisvísinum og bætum loks við fastanum C.

      Prófum þessa niðurstöðu.

         F´(x) = f(x) = (n+1)x^n+1–1/(n+1) + 0 = xⁿ

      Þetta passar.

Sýnidæmi 3

Finnum það stofnfall fallsins f(x) = 3x² – 2x + 1 sem sker punktinn (1, 1).

   F(x) = 3x³/3 – 2x²/2 + x + C = x³ – x² + x + C

Prófum með deildun.

   F´(x) = 3x² – 2x + 1 + 0

Þetta passar og þá er næst að finna fasta C sem er þannig að grafið hitti á punktinn (1, 1). Við notum okkur að F(1) hlýtur að vera 1.

   F(1) = 1³ – 1² + 1 + C = 1 + C

Ef 1 á að koma út úr þessu þá verður C að vera 0. Stofnfallið sem við leitum að er þá

   F(x) = x³ – x² + x

Sýnidæmi 4

Finnum þau stofnföll fallanna f(x) = e^x og g(x) = e^2x sem skera punktinn (0, 0).

Fallið f(x) = e^x hlýtur að hafa stofnfallið F(x) = e^x + C og auðvelt er að fullvissa sig um það með deildun, en finnum fastan C.

   F(0) = 0 = e⁰ + C = 1 + C

Til þess að 0 komi út verður C að vera –1.

   F(x) = e^x – 1

Fallið g(x) = e^2x hlýtur að hafa stofnfall sem er eitthvað form af e^2x. Deildun á e^2x gefur 2e^2x vegna þess að við verðum að margfalda með afleiðu innra fallsins (sem er 2x). Hér hljótum við því að deila með 2 í stað þess að margfalda í deilduninni. Gerum það og prófum niðurstöðuna.

   G(x) = e^2x/2 + C

   G´(x) = g(x) = 2e^2x/2 + 0 = e^2x

Þetta passar þannig að við höfum fengið út eftirfarandi reglu:

   Fallið f(x) = e^kx hefur stofnfallið .

 þá getum við hafist handa við að finna fastann C.

   G(0) = 0 = e⁰/2 + C = ½ + C

Til þess að 0 komi út verður C að vera –½.

   G(x) = ½e^2x – ½

Sýnidæmi 5

Finnum stofnfall f(x) = a^x.

Tökum logra af báðum hliðum til þess að geta umritað fallið yfir á formið e^kx.

   ln f(x) = ln a^x = x·ln a          Hér notum við regluna ln a ^b= b·ln a.

Setjum nú báðar hliðar sem veldi á e.

   e^{ln f(x)} = e^{x·ln a}

      f(x) = e^{x·ln a}

Nú getum við notað niðurstöðuna úr sýnidæmi 4, regluna , vegna þess að ln a er föst stærð = "k".

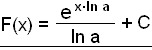
Nú getum við farið sömu leiðina til baka og umritað e^{x·ln a} yfir á formið a^x.

Sýnidæmi 6

Finnum stofnföll hornafallanna f(x) = sin x, g(x) = cos x og h(x) = cos 2x.

Nú er f´(x) = cos x og g´(x) = –sin x þannig að líklegt er að stofnföllin séu sams konar víxlun. Ef við prófum cos x sem stofnfall f(x) og deildum þá fáum við vitlaust formerki. Ef við hins vegar prófum sin x sem stofnfall g(x) þá fáum við rétta niðurstöðu. Stöfnföllin eru því eftirfarandi:

   F(x) = –cos x + C

   G(x) = sin x + C

Snúm okkur loks að fallinu h(x) = cos 2x. Ef við giskum á stofnfallið H(x) = sin 2x þá sjáum við að afleiða þess, h(x) = 2·cos 2x, verður tvöfallt hærri en við vonuðumst til vegna þess að það er margfaldað með afleiðu innra fallsins (sem er 2x). Við verðum því að deila með tveimur í ágiskunina okkar.

   H(x) = ½·cos 2x + C

Sýnidæmi 7

Skoðum nú nokkur dæmi um stofnföll rótafalla. Við skulum breyta þeim í brotin veldi og nota niðurstöðuna úr sýnidæmi 3 þar sem við fundum að f(x) = xⁿ hefði stofnfallið

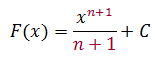
1)   Finnum stofnfall f(x) = .

      Breytum þessu í

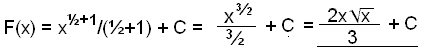
2)   Finnum stofnfall .

       Breytum þessu í

3)   Finnum stofnfall .

       Breytum þessu í .

Sýnidæmi 8

Finnum stofnfall f(x) = 1/x.

Hér er eðlilegt að breyta þessu í veldisstærð eins og við höfum gert áður, en nú gengur það ekki.

   f(x) = x^–1

   F(x) = x^–1+1/(–1+1) = x⁰/0

Þetta er ekki nothæft svar þannig að við verðum að grafa upp eitthvað fall sem hefur afleiðuna 1/x og þá rámar okkur í eftirfarandi:

   (ln x)´ = 1/x

Þetta segir okkur að stofnfall f(x) = 1/x hlýtur að vera ln x. Hér þurfum við þó að gæta að okkur vegna þess að f(x) = 1/x getur tekið við öllum tölum nema núlli (F_f = R\ {0}. Ln x er hins vegar aðeins skilgreint fyrir jákvæðar tölur þannig að við verðum að einskorða okkur við tölugildið af x. Svarið verður því eftirfarandi:

   F(x) = ln ІxІ + C

Æfðu þig á þessum aðferðum og taktu síðan próf 1 í Heildun.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum