© 2006  Rasmus ehf og Jóhann Ísak Pétursson

Jöfnur II kynning 5

Jöfnuhneppi

Jafnan x − y = 1 inniheldur tvær óþekktar stærðir (breytur). Lausnir á henni eru öll talnapör sem munar einum á svo sem 2 og 1, 3 og 2 , 4 og 3 o.s.frv.

Ef við viljum negla niður svar sem er nákvæmlega eitt par af tölum þá verðum við að fá til viðbótar nýja jöfnu sem sýnir annað samhengi á milli x og y,  t.d. x + y = 3, en 2 og 1 er eina talnaparið sem uppfyllir skilyrði beggja jafnanna.

Jöfnupar af gerðinni

nefnist jöfnuhneppi með tveimur óþekktum.

Að finna lausn jöfnuhneppa felst í því að finna talnapar sem uppfyllir skilyrði beggja jafnanna. Við skulum nú líta á helstu aðferðirnar til þess.

Sýnidæmi 1

Samlagningaraðferðin

Leysum jöfnuhneppið

með samlagningaraðferð.

Ef við leggjum saman jöfnurnar þá dettur y út og við finnum lausn fyrir x.

Við sjáum að x = 2

Ef við setjum 2 í stað x í annarri jöfnunni þá getum við reiknað út y
Lausnin er þá (2,1)  eða x = 2 og y = 1

 

Sýnidæmi 2 Innsetningaraðferðin

Leysum jöfnuhneppið

 

 með innsetningaraðferð. 

  x − y = 1

        x = 1 + y

Við leysum fyrri jöfnuna m.t.t. x.

Síðan setjum við lausnina inn fyrir x í seinni jöfnunni

1 + y + y = 3

            2y = 3 − 1 = 2

              y = 1

og finnum y = 1.

x + 1 = 3

      x = 2		 Loks setjum við 1 í stað y í annarri jöfnunni og finnum að x = 2

 

Afbrigði af innsetningaraðferðinni er að leysa báðar jöfnurnar m.t.t. y en þá má setja jafnaðarmerki á milli hægri hliða jafnanna.

Sýnidæmi 3 Innsetningaraðferðin (afbrigði)

x − y = 1 gefur y = x − 1

x + y = 3 gefur y = 3 − x

Þá er x − 1 = 3 − x

               2x = 3 + 1 = 4
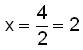og y = 2 − 1 = 1   lausnin (2,1)

 

Skoðum nú aðeins flóknara dæmi.
Sýnidæmi 4  

Leysum jöfnuhneppið

  með samlagningaraðferðinni

Hér gengur ekki að nota samlagningu beint.

  

 En ef við margföldum efri jöfnuna fyrst með tveimur og leggjum svo saman þá dettur y út.

Við reiknum síðan út x og fáum x = 2

    2∙2 + y = 7

             y = 7 − 4 = 3

 Setjum lausnina á x inn í seinni jöfnuna og reiknum út y.

Lausnin er þá x = 2 og y = 3   ( 2,3)

Með innsetnigaraðferð verður þetta svona:

   2x + y = 7

           y = 7 − 2x

 Einföldum fyrri jöfnuna með tilliti til y
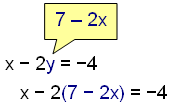Setjum smasvörun fyrir eitt y inn í seinni jöfnuna.

   x − 14 + 4x = −4

  5x = −4 + 14 = 10

 Drögum saman samskonar liði

og reiknum út að x = 2
y = 7 − 2x = 7 − 2∙2 = 3 Setjum lausnina á x inn í fyrri jöfnuna og reiknum út y.

Lausnin er þá x = 2 og y = 3   ( 2,3)

Sýnidæmi 5      

Skoðum nú hvernig þetta er gert í grafískri reiknivél af Casio-gerð.

Við byrjum á því að velja jöfnulausnir (EQUA) á forsíðuvalmyndinni.

Í valmynd sem kemur upp veljum við línulegar jöfnur (simultaneous) með F1.

 
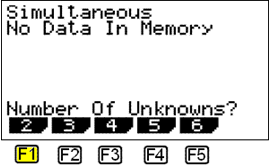Síðan veljum við tvær óþekktar með F1 á þessari valmynd.

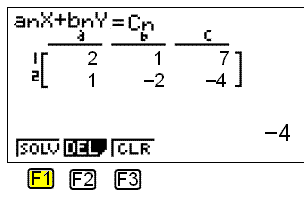Í þeirri valmynd sem nú opnast þurfum við að slá inn tölustuðlana í jöfnuhneppinu.

Fyrir jöfnuna 2x + y = 7 sláum við inn stuðlana 2, 1 (fyrir eitt y) og 7, og fyrir jöfnuna x − 2y = −4 sláum við inn 1, −2 og −4.

Runa aðgerða verður eftirfarandi:

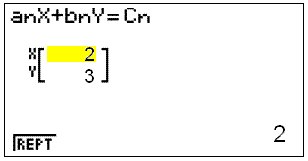Að lokum veljum við F1 til þess að fá lausnirnar, en þær koma fram á valmyndinni hér til vinstri:

Eða x = 2 og y = 3

Æfðu þig á þessum aðferðum og taktu síðan próf 5. í Jöfnum II.

ps. mundu eftir að fylla út í tékklistann þinn jafnóðum.