© 2000  - 2010  Rasmus ehf

Margföldun og deiling brota  Kynning 1

Stytting og einföldun brota

 Rifjum aðeins upp þætti talna.

Dæmi talan 6 = 2 · 3    við segjum þá að talan 6 hafi marföldunarþættina 2 og 3. Allar heilar tölur eiga sér margföldunarþætti, tvo eða fleiri nema þær tölur sem nefndar eru Prímtölur dæmi: (2,3,5,7,11,13,17,19,23.......o.s.frv.)

Talan 1 er áhrifslaus í margföldun því er hún aldrei notuð sem þáttur.

Mundu að brotastrik þýðir alltaf deiling.

Skoðum nokkur dæmi um hvernig hægt er að nota sér sameiginlega þætti til að stytta brot.

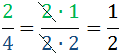                            Við sjáum að 2 = 2·1 og að 4 = 2·2 

Talan 2 er sameiginlegur þáttur ( 2:2 = 1)  Við styttum sameiginlegan þátt út út brotinu.

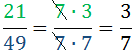                        Við sjáum að 21 = 7·3 og að 49 = 7·7 

Talan 7 er sameiginlegur þáttur , við styttum sameiginlegan þátt út út brotinu.

      Ef prímtölur, þá gengur ekkert uppí þeim nema talan sjálf og 1.

Því enginn sameiginlegur þáttur, óstyttanlegt brot.

Margföldun brota

Stundum  er unnið með heilar tölur og brot.

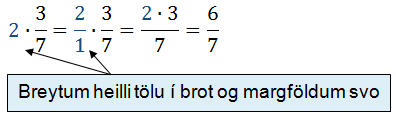   Heila talan margfaldist bara uppá strikinu.

Brot margfaldað með broti (ekkert samnefnarkjaftæði hér).

Blandaðar tölur í margföldun:

Dæmi: þú margfaldar heilu töluna með nefnara og bætir teljaranum við.

1 · 3 + 1 = 4      og setur útkomuna í sæti teljarans. Nefnarinn er áfram sá sami.

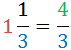
Við þurfum að kunna að breyta blandaðri tölu  í brot.

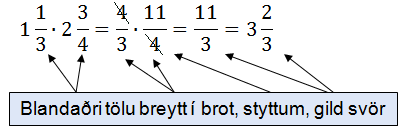
Við breytum fyrst í brot, styttum og einföldum.

Ath. það má svara á mismunandi vegu.

Deiling brota

Ef deiling brota þá snúum við seinna brotinu og vinnum dæmið sem margföldun.

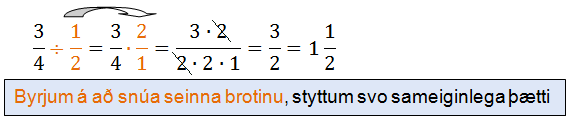
Heilar tölur þarfa að laga til.

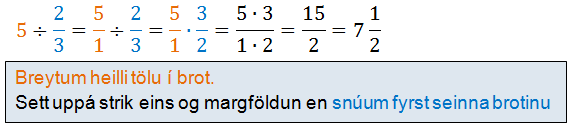
Blandaðar tölur eru ónothæfar nema laga þær til.

Taktu nú próf 1. í Margföldun og deilingu brota.