© 2010  Rasmus ehf    og Jóhann Ísak

Funksjoner 2

 

Introduksjon 3

Rasjonale funksjoner og asymptoter

En funksjon på formen hvor t(x) og n(x) er polynomer, kalles en rasjonal funksjon.

Grafen til en rasjonal funksjon kan gjenkjennes ved at de ofte deler seg inn i to eller flere deler. Disse delene går ut av koordinatsystemet langs en imaginær rett linje kalt en asymptote.

La oss se på funksjonen   

Denne grafen følger en horisontal asymptote med y = 1 (rød i diagrammet over) når den går ut av koordinatsystemet på høyre og venstre side. Når x går mot verdiene 1 og –1, følger grafen vertikale linjer (blå) ut av koordinatsystemet. Disse vertikale asymptotene oppstår når nevneren, n(x), går mot null.
 For å finne likningene til de vertikale asymptotene, må vi løse likningen:

   x2 – 1 =  0

         x2 = 1

          x = 1 or x = –1

Når x går mot 1 eller –1, går grafen nesten rett opp eller rett ned, og funksjonsverdien går mot  +∞ eller –∞.

Vi får en horisontal asymptote fordi teller og nevner, t(x) = x2 og n(x) = x2 – 1 nærmer seg hverandre når absoluttverdien av x øker.
Hvis x = 100, blir x2 = 10000 og x2 – 1 = 9999. Hvis vi deler den ene på den andre, får vi tilnærmet 1. Jo større x - verdi, jo nærmere kommer vi 1.

Vi kan finne vertikale asymptoter ved å løse likningen      n(x) = 0 hvor n(x) er nevneren i funksjonen(gjelder ikke hvis telleren t(x) blir null for samme x - verdi).

Horisontale asymptoter finner vi ved grenseverdien

Eksempel 1

Finn asymptotene til funksjonen .

For å finne den vertikale asymptoten, løser vi likningen

   x – 1 = 0

         x = 1

Grafen har en vertikal asymptote med likningen  x = 1.

For å finne den horisontale asymptoten, regner vi ut   .

Telleren er 1 uansett x - verdi. Det betyr at jo større nevneren blir, jo mindre blir brøken. Hvis x = 1000, blir f(x) = 0,001. Når x går mot uendelig, går   f(x) mot null.

Dette forteller oss at  y = 0 (y - aksen) er en horisontal asymptote.

Tegn til slutt grafen på en kalkulator for å bekrefte resultatene.

I eksempelet over fant vi en enkel regel:
 En rasjonal funksjon hvor telleren har høyere eksponent enn nevneren, har x - aksen som en horisontal asymptote.

 

Eksempel 2

Finn asymptotene til  .

Nevneren kan aldri gå mot null, og funksjonen har derfor ingen vertikale asymptoter.

   x2 + 1 = 0

         x2 = –1 har ingen løsning

Nå ser vi på hva som skjer når x blir uendelig stor:

Vi deler teller og nevner på den høyeste potensen av x i funksjonen.

Del teller og nevner på x2 og forkort.
Brøker hvor x er i nevner, og ikke i teller, går mot 0.

Grafen har en horisontal asymptote y = 2.

Nå skal vi tegne grafen på kalkulatoren.

 Velg først GRAPH i hovedmenyen.

Skriv deretter inn funksjonen. Husk parenteser som på bildet under.

Vi får dette bildet på kalkulatoren. Grafen krysser faktisk asymptoten! Dette kan aldri skje med en vertikal asymptote.

Eksempel 3

Nå et eksempel hvor telleren er opphøyd i en høyere potens enn nevneren.

  . Telleren er et andregrads polynom, mens nevneren er i første grad.

Vi ser først etter vertikale asymptoter:

   x – 1 = 0

         x = 1        

Grafen har en vertikal asymptote med likningen  x = 1.

Vi deler telleren på nevneren

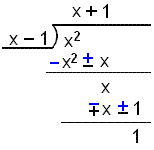
Vi skriver om f(x):

Vi vet at  , som betyr at  f(x) ≈ x + 1 når x går mot uendelig.

Dette forteller oss at  y = x + 1 er en skrå asymptote.

Grafen vises under.

Vi skal følge denne tankegangen videre. Hvis tellerens eksponent hadde vært to grader høyere enn nevnerens, ville grafen ha fulgt en parabel ut av koordinatsystemet.

 

Eksempel 4

Finn asymptotene til funksjonen .

Her slipper vi å dele, og vi ser med en gang at det finnes en skrå asymptote med likningen y = x.

Vi løser likningen n(x) = 0 for å finne de vertikale asymptotene.

   x2 – 1 = 0

         x2 = 1

          x = 1 or x = –1

De vertikale asymptotene er x = 1 og x = –1.

Her er grafen

 

Oppsummering

 1)  Vertikale asymptoter kan oppstå når nevneren går mot null.
       Løs likningen n(x) = 0 for å finne dem.

 2)  Hvis den høyeste eksponenten i nevneren n(x) er større enn den høyeste eksponenten i telleren t(x), fungerer x - aksen som horisontal asymptote.

3)  Hvis den høyeste eksponenten i nevneren n(x) er den samme som den høyeste eksponenten i telleren t(x), finner vi asymptoten ved å regne ut grenseverdien
        .
4)  Hvis den høyeste eksponenten til nevneren n(x) er 1 lavere enn den høyeste eksponenten til telleren t(x), kan vi finne likningen til den skrå asymptoten ved divisjon.

Se på eksemplene, og regn deg gjennom test 3 i Funksjoner 2.
Husk å fylle ut sjekklisten underveis.