© 2008 Rasmus ehf og Jóhann Ísak Pétursson
Likninger III
© 2008 Rasmus ehf og Jóhann Ísak Pétursson |
Likninger III |
|
Nå skal vi se på hvordan man løser kvadratiske likninger (andregradslikninger). Løsningen til en andregradslikning forteller oss hvor andregradslikningen
f(x) = ax2 + bx + c krysser x-aksen.
Først skal vi se på likninger hvor en av koeffisientene b eller c er null (b = 0 eller c = 0).
Eksempel 1
| a) 2x2 − 8 = 0 2x2 = 8 x2 = 4 x = ±2 |
Først flytter vi konstantleddet til den andre siden av likhetstegnet. Så deler vi begge sider på to. Til slutt tar vi kvadratroten av begge sider. Husk at løsningen kan være både negativ og positiv. |
| b) 2x2 + 8 = 0 2x2 = −8 x2 = −4 ingen løsning |
Her kan vi ikke finne kvadratroten på grunn av minustegnet, og likningen kan ikke løses. |
Eksempel 2
| a) 2x2 − 8x = 0 2x(x − 4) = 0 2x = 0 eller x − 4 = 0 x = 0 eller x = 4 |
Faktoriser ved å sette 2x utenfor en parentes. For at venstre side skal bli null, må en av faktorene være null. |
| b) 2x2 + 8x = 0 2x(x + 4) = 0 2x = 0 eller x + 4 = 0 x = 0 eller x = −4 |
Igjen får vi to løsninger. Kvadratiske likninger med c=0 får alltid to løsninger. |
Hvis ingen av koeffisientene a, b eller c er null, blir det vanskeligere.
Hvis du kan få en likning til å passe inn i denne formelen, er den lett å løse:
p2 ± 2pq + p2 = (p ± q)2
Eksempel 3
| a) x2 + 2x + 1 = 0 (x + 1)2 = 0 (x + 1) = 0 x = −1 |
Denne likningen passer rett inn i formelen. |
| b) 2x2 − 8x + 8 = 0 2(x2 −4x + 4) = 0 2(x – 2)2 = 0 (x − 2) = 0 x = 2 |
Her må vi sette 2 utenfor en parentes for å få likningen til å passe inn i formelen. |
Noen ganger kan vi faktorisere likningen ved å finne faktorer som passer,
og finne x-verdien som gjør at hver faktor blir null.
Eksempel 4
Løs likningen x2 − 5x + 6 = 0
x2 − 5x + 6 = 0
(x − 2)(x − 3) = 0
x = 2 eða x = 3
Eksempel 5
| Løs likningen x2 − 4x − 5 = 0.
x2 − 4x − 5 = 0 x2 − 4x + 22 − 22 − 5 = 0 (x2 − 4x + 4) − 9 = 0 |
Her legger vi til (og trekker samtidig fra) halve koeffisienten til b, opphøyd i annen. Så kan vi bruke formelen p2± 2pq + q2 = (p ± q)2 |
(x − 2)2 − 9 = 0  |
Resultatet er på formen (x + r)2 + s |
x − 2 = ±3 x = 2 ± 3 x = 5 eða x = −1 |
…og vi gjør som før. |
Eksempel 6
Løs likningen 3x2 − 24x + 21 = 0
3(x2 − 8x) + 21 = 0
3(x2 − 8x + 42) − 3∙42 + 21 = 0
3(x − 4)2 − 48 + 21 = 0
3(x − 4)2 = 27
(x − 4)2 = 9
x − 4 = ±3
x = 4 + 3 = 7 eða x = 4 − 3 = 1
Eksempel 7
Nå skal vi finne en formel som vi kan bruke til å løse en hvilken som helst andregradslikning på formen ax2 + bx + c = 0
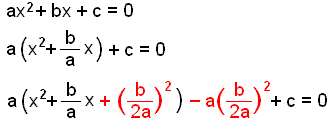 |
Sett a utenfor en parentes. Legg til kvadratet av halve koeffisienten til x. Trekk fra det samme tallet, og husk å gange med a. Skriv de tre første leddene som en parentes i annen. |
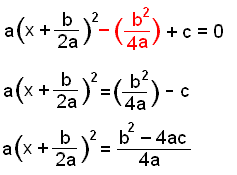 |
Flytt de siste to leddene til den andre siden av likhetstegnet, og finn fellesnevneren. |
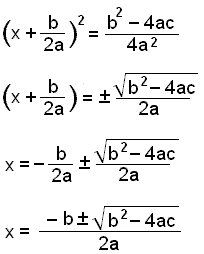 |
Ta kvadratroten av begge sider av likningen, og husk at svaret kan ha negativt fortegn. Finn til slutt x ved å flytte leddet inne i parentesen til den andre siden av likhetstegnet. |
Dette var ganske komplisert algebra. Men nå som vi har funnet formelen, trenger vi ikke å gjøre det samme igjen. Vi kan bruke formelen til å løse alle kvadratiske likninger.
Formelen kan brukes til å løse likningen ax2 + bx + c = 0
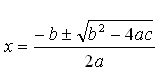 |
Dette er en av de mest kjente og brukte matematiske formlene.
Eksempel 8
Nå skal vi bruke formelen til å løse likningen
2x2 − 10x + 8 = 0
Koeffisientene er: a = 2
b = −10
c = 8
Sett tallene for a, b og c inn i formelen
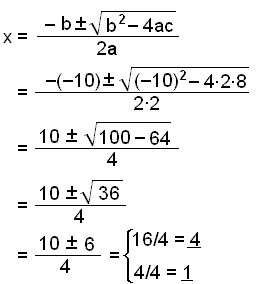
Eksempel 9
Løs likningen x2 − 3x + 6 = 0
Koeffisientene er a = 1, b = −3 og c = 6. Sett dem inn i formelen.
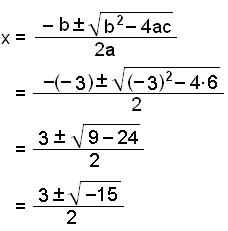
Her er det et negativt tall under rottegnet, og likningen har ingen løsning.
Eksempel 10
Vi kan også
løse grafiske likninger ved hjelp av en grafisk kalkulator. 
Slik løser man likningen 2x2 − 10x + 8 = 0 på en grafisk kalkulator:
Gå først til „EQUA“ fra hovedmenyen.
Du får opp dette vinduet:
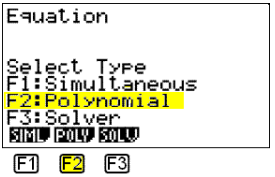
Velg „Polynomial“ med F2 .

Velg 2, fordi likningen er av andre grad (trykk F1). Hvis vi skulle løse en tredjegradslikning, hadde vi valgt 3. Du får opp dette vinduet:
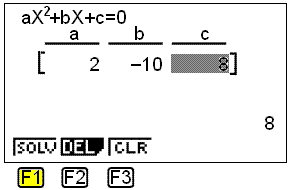
Vi setter inn verdiene a = 2, b = −10 og c = 8 ved å trykke EXE mellom hvert tall.
Trykk knappene i denne rekkefølgen:
![]()
Til slutt velger vi SOLV ved å trykke F1. Løsningene 4 og 1 kommer frem på skjermen:
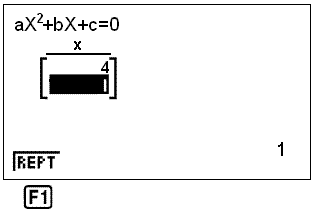
Eksempel 11
Nå skal vi se på hva kalkulatoren gjør med likninger som ikke har noen løsning. Vi tar for oss likningen x2 − 3x + 6 = 0. Vi skriver inn a = 1, b = −3 and c = 6. Kalkulatoren gir følgende svar:
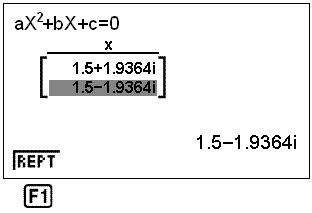
Dette betyr at svaret er et imaginært tall. Det finnes ingen løsning i reelle tall.
Eksempel 12
Nå skal vi løse en kvadratisk
likning ved hjelp av EXCEL.
Vi skal løse likningen 2x2 − 10x + 8 = 0.
Skriv inn a, b og c in cellene A3, B3 og C3.
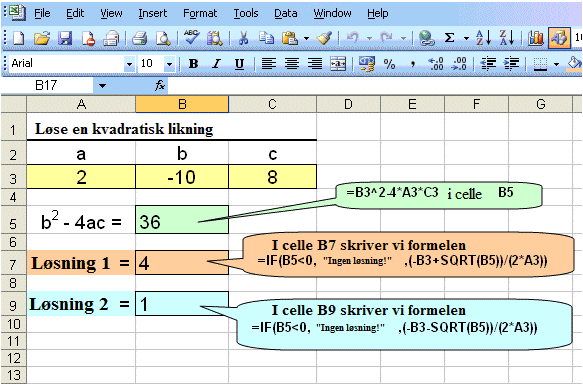
Hvis vi bruker programmet til å løse en likning med bare en løsning, som for eksempel x2 − 2x + 1 = 0, får vi det samme svaret to ganger.

Hvis likningen ikke har noen løsning, som likningen
x2 − 3x + 6 = 0 vil EXCEL vise dette:

Prøv test 1 i Likninger III.
Husk å bruke sjekklisten for å få oversikt over hva du har gjort.