© 2010  Rasmus ehf    og Jóhann Ísak

Vektorer

Introduksjon 5

Vektorer og linjer

Eksempel 1

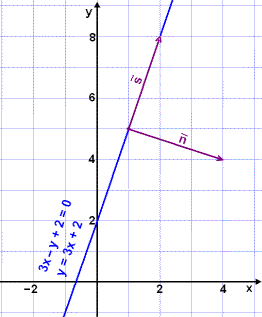
Vi skal finne en vektor på linjen y = 3x + 2 og en annen vektor som står vinkelrett på linjen.

Vi begynner med å finne to punkter på linjen.

   Vi velger x = 0 og regner ut y. Vi får y = 3·0 + 2 = 2.

   (0, 2) er på linjen.

   Vi velger x = 1 og regner ut y. Vi får y = 3·1 + 2 = 5.

   (1, 5) er på linjen.

Vi skal finne vektoren mellom de to punktene. Vektoren har samme retning som linjen. Den er derfor en retningsvektor for linjen, og vi kaller den . Vi roterer vektoren 90° og får en vektor som er vinkelrett med linjen. Den kalles en normalvektor, . På bildet til høyre kan vi se linjen og vektorene.

Vi kan skrive om likningen for linjen, y = 3x + 2, til 3x – y + 2 = 0 ved å flytte y til den andre siden av likhetstegnet. Dette kalles normalformen, og vi ser at koeffisientene 3 og  –1 er de samme som i normalvektoren . 

Nå skal vi undersøke om dette gjelder generelt.

Vi har linjen ax + by + c = 0.

Vi finner to punkter på linjen ved å sette x = 0 og regne ut y, og deretter sette y = 0 og regne ut x.

   a·0 + by + c = 0

                    y = –^c/b og x = 0

   ax + b·0 + c = 0

                    x = –^c/a og y = 0

Punktene (0, –^c/b) og (–^c/a, 0) er på linjen.

Linjens retningsvektor blir da og normalvektoren .

Det kan være vanskelig å lese koordinatene når de står i brøkform, så vi multipliserer dem med ab/c. Dette endrer retningene på vektorene, men de er fortsatt retningsvektor og normalvektor for den samme linjen.

     og

For å finne retningsvektoren og normalvektoren til en linje, skriver vi linjens likning på generell form, og leser av koordinatene for linjens retningsvektor og normalvektor.

Med det vi akkurat har lært, kan vi finne vinkelen mellom to linjer, hvis vi bruker skalarproduktet mellom linjenes retningsvektorer. Vi kan også finne vinkelen mellom linjene ved hjelp av normalvektorene og deres skalarprodukter, fordi det er like stor vinkel mellom normalvektorene som mellom retningsvektorene.

Eksempel 2

Vi skal finne vinkelen vº mellom en linje l₁ med likningen y = 3x + 2 og en linje l₂ med likningen y = x + 4 (se bildet).

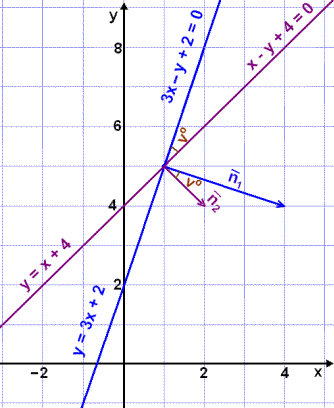
   Linjenes likninger på normalform er3x – y + 2 = 0 og x – y + 2 = 0.

   Linjenes normalvektorer er og

Vi regner ut lengden av normalvektorene.

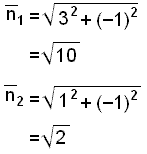
Nå kan vi bruke skalarproduktet til å regne ut vinkelen vº mellom normalvektorene. Denne vinkelen er like stor som vinkelen mellom linjene.

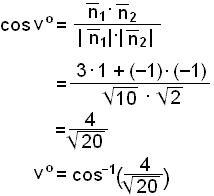
          vº ≈ 26,6º

Hvilke av vektorene som starter i  (1, 2) er

vinkelrette med vektoren ?

Hvis vi kaller endepunktet (x, y), passer alle vektorer med koordinatene .

Ettersom skalarproduktet til to vinkelrette vektorer er 0, kan vi sette opp denne likningen:

   3(x – 1) + (–1)(y – 2) = 0

              3x – 3 – y + 2 = 0

                    3x – y – 1 = 0

Dette er likningen på normalform for en linje som går gjennom punktet (1, 2) og har normalvektoren .

Nå har vi en metode for å finne likningen til en linje ut fra et punkt og normalvektoren.

Hvis punktet (x₁, y₁) er på en linje med normalvektoren , er likningen på normalform slik:

Eksempel 3

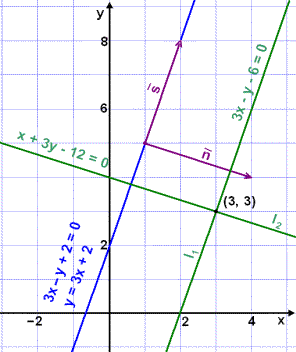
Vi skal finne likningene for linjene l₁ og l_2, som skjærer hverandre i punktet (3, 3). l₁
er parallell med linjen 3x –y + 2 = 0, og l₂ er vinkelrett med den.

  Normalvektoren til l₁ er den samme som for linjen 3x –y + 2 = 0, nemlig . Vi kan derfor bruke koordinatene i likningen til linjen.

     a(x – x₁) + b(x – y₁) = 0

   3(x – 3) + (–1)(y – 3) = 0

              3x – 9 – y + 3 = 0

                     3x – y – 6 = 0         (likningen til l₁)

  Normalvektoren til l₂ er retningsvektoren til linjen 3x –y + 2 = 0, eller . Vi kan derfor bruke koordinater direkte i likningen til linjen.

     a(x – x₁) + b(x – y₁) = 0

       1(x – 3) + 3(y – 3) = 0

              x – 3 + 3y – 9 = 0

                  x + 3y – 12 = 0         (likningen til l₂)

Vi ser på en tegning av linjene.

Eksempel 4

Vi skal regne ut avstanden mellom de parallelle linjene 3x – y + 2 = 0 og 3x – y – 6 = 0 (se bildet).

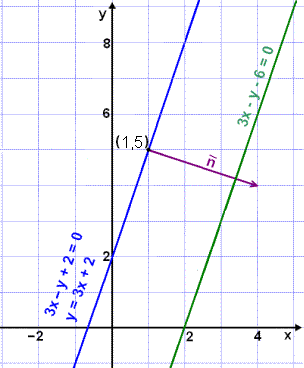
Vi velger punktet (1, 5) på linjen 3x – y + 2 = 0 og regner ut avstanden fra punktet til en annen linje 3x – y – 6 = 0.
På denne måten finner vi avstanden mellom linjene.

Vi ser på bildet at normalvektoren er lenger enn avstanden mellom linjene. Vi må finne et tall t som vi kan multiplisere med slik at vektoren blir nøyaktig like lang som avstanden mellom linjene, og endepunktet (x, y) er på linjen. Vi kan sette opp denne likningen:

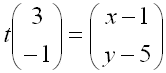
Dette gir oss to likninger som vi kan løse med hensyn på x og y.

   3t = x – 1          og          –t = y – 5

     x = 3t + 1                         y = –t + 5

Deretter setter vi inn for x og y.

                       3x – y – 6 = 0

   3(3t + 1) – (–t + 5) – 6 = 0  

         9t + 3 + t  – 5 – 6 = 0 

                               10t = 8

                                   t = 0,8

I eksempel 2 regnet vi ut lengden av vektoren , og fikk svaret .

Avstanden mellom linjene er derfor t·, eller 0,8·.

Nå skal vi regne gjennom eksempelet over med bokstaver, så vi får en generell formel for avstanden mellom et punkt og en linje.

    Linjens likning på normalform er ax + by + c = 0, og punktet vi velger har koordinatene(x₁, y₁). Vi kan 
     sette opp en likning:

    Det gir oss to nye likninger, som vi løser med hensyn på x og y.

         ta = x – x₁          og          tb = y – y₁

          x = ta + x₁                        y = tb + y₁

    Vi setter inn i den opprinnelige likningen, og setter t utenfor parentesen.

                              ax + by + c = 0

         a(ta + x₁) + b(tb + y₁) + c = 0

           ta² + ax₁ + tb² + by₁ + c = 0

                                    ta² + tb² = –ax₁ – by₁ – c

                                   t(a² + b²) = –ax₁ – by₁ – c

   Vi vet at ||² = a² + b², så vi kan skrive om formelen:

         t·||² = –ax₁ – by₁ – c

    Hvis vi deler med ||² på begge sider av likhetstegnet, finner vi t, som vi ganger med lengden på normalvektoren . Vi måler lengden i absoluttverdier, fordi den ikke kan være negativ.

       t = |–ax₁ – by₁ – c| /||²

    Vi multipliserer med ||.

Eksempel 5

Vi skal speile punktet  (–3, 5) om linjen 3x – y – 6 = 0.

Vi finner først en vektor som er vinkelrett med linjen 3x – y – 6 = 0, begynner i punktet (–3, 5) og har endepunktet P = (x, y) på linjen. Dette er normalvektoren t (se bildet). Det speilede punktet S finner vi deretter ved å addere vektoren t med vektoren fra O til P.

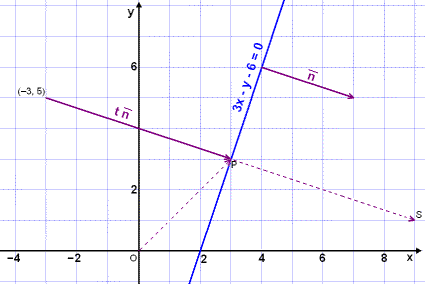
Vi må først finne t. Vi kan sette opp disse likningene:

Vi får to likninger, som vi løser med hensyn på x og y.

   3t = x + 3        og        –t = y – 5

    x = 3t – 3                    y = –t + 5

Vi setter løsningene inn i likningen, og løser for t.

                      3x – y – 6 = 0

   3(3t – 3) – (–t + 5) – 6 = 0

            9t – 9 + t – 5 – 6 = 0

                                 10t = 20

                                     t = 2

Vi får da vektoren , og vi kan regne ut koordinatene til P.

Hvis vi legger 2  til denne vektoren, får vi vektoren fra O til S.

Koordinatene til det nye punktet S = (9, 1).

Eksempel 6

Vi skal finne likninger for linjene l₁ og l₂ som skjærer hverandre i punktet (3, 4) og er parallell med vektorene og .

Vi skal deretter finne en halveringslinje som deler vinkelen mellom linjene i to like store vinkler.

Normalvektorene til linjene l₁ og l₂ er og

Likningen til l₁ blir då

   1(x – 3) – 3(y – 4) = 0

        x – 3 – 3y + 12 = 0

             x – 3y + 9 = 0

og likningen til l₂ blir

   3(x – 3) – 1(y – 4) = 0

          3x – 9 – y + 4 = 0 

              3x – y – 5 = 0.

På halveringslinjen ligger alle punktene (x, y) som har samme avstand til linjene l₁ og l₂. Vi kan derfor finne likningen for halveringslinjen ved å sette opp avstandsformelen for avstanden til (x, y) fra begge linjene. Siden avstanden er den samme til begge linjene, kan vi sette likhetstegn mellom avstandsformlene.

–x + 3y – 9 = ±(–3x + y + 5)

± på grunn av absoluttverditegnet

Dette gir oss to likninger:

   –x + 3x + 3y – y – 9 – 5 = 0    og  –x – 3x + 3y + y – 9 + 5 = 0

                     2x + 2y – 14 = 0                              –4x + 4y – 4 = 0

                           x + y – 7 = 0                                    x – y + 1 = 0

Vi får to svar fordi det finnes to vinkler mellom linjene l₁ og l₂  (se bildet).

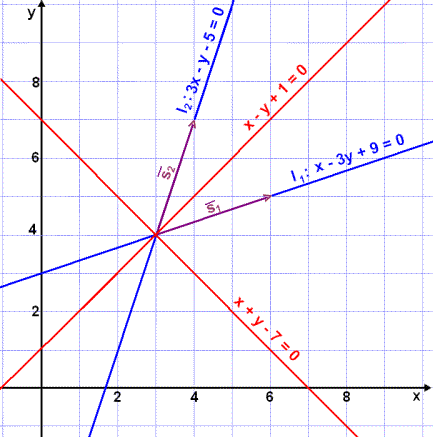
Øv på eksemplene, og regn deg gjennom Test 5 i Vektorer.

Husk å fylle ut sjekklisten underveis.