Introduksjon 4

 Rasjonale funksjoner

Rasjonale funksjoner skrives på denne formen:

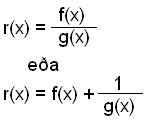eller

Hvor både f(x) og g(x) er polynomer, og nevneren, g(x), er av minst 1. grad (inneholder x)

Nå skal vi se på noen eksempler på rasjonale funksjoner og grafene deres.

Eksempel 1

Først ser vi på

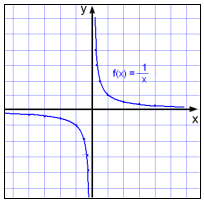
Hvis vi lager en verditabell, ser vi med en gang at x ikke kan være 0, fordi det ikke går an å dele på 0.

Etter hvert som x nærmer seg verdien 0, men fortsatt er positiv (x= 0,1 , x = 0,01 osv.), ser vi at funksjonsverdien (y) blir større og større (x = 0,01 gir y = 100).

Når x nærmer seg 0 på den negative siden (x = −0.1, x =− 0.01 osv), får funksjonsverdien en mer og mer negativ verdi ( x = −0.01 gir y = −100).

Grafen til funksjonen ser ut til å være nesten parallell med y-aksen i nærheten av der hvor x er 0.

Når dette skjer, har funksjonen en vertikal asymptote.

Likningen til asymptoten er x = 0.

Eksempel 2

Nå skal vi se på funksjonen

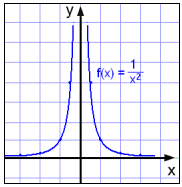
Vi ser at funksjonsverdien blir større og større etter hvert som x nærmer seg 0 fra høyre ( x > 0 ) og fra venstre ( x < 0 ).

Igjen er y-aksen en vertikal asymptote.

V ser også at grafen verken skjærer x-aksen eller y-aksen.

Vi kan prøve å regne ut skjæringspunktene og se hva som skjer.

Først finner vi ut hvor grafen krysser y-aksen ved å regne ut f(0), fordi x-koordinatet til alle punkter på y-aksen er 0.

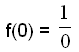
For å regne ut dette, må vi dele på 0, noe som er umulig.

For å finne ut hvor grafen krysser x-aksen må vi løse likningen f(x) = 0 eller y = 0 fordi alle punktene på x-aksen har y-koordinatet 0.

Igjen får vi en likning som ikke har noen løsning. Derfor kan vi konkludere at grafen ikke krysser verken x- eller y-aksen.

Eksempel 3

Se på funksjonen

Og regn ut hvor grafen krysser aksene.

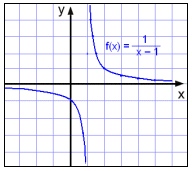
Hvis x=1, må vi dele på 0. Derfor er x ≠ 1. Etter hvert som x nærmer seg 1 vil y-verdien bli større og større. Den blir positiv hvis x>1 og negativ hvis x<1. 

Denne gangen ser grafen ut til å ligge nærme linjen i x=1, mens den går opp når x > 1 og ned når x < 1.

For å finne ut hvor grafen krysser y-aksen, regner vi ut f(0), fordi x=0 på y-aksen.

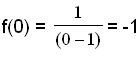
For å finne ut hvor grafen krysser x-aksen løser vi likningen f(x) = 0 eller y = 0 fordi alle punktene på x-aksen har y=0.

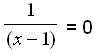
1 = 0∙(x − 1) = 0

Igjen får vi en likning som ikke har noen løsning, så vi kan konkludere med at grafen ikke krysser x-aksen.

Eksempel 4

Se på funksjonen

Og finn ut om det er noen skjæringspunkter med koordinataksene.

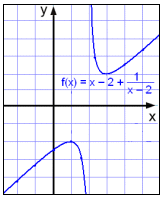
Vi ser at x ≠ 2, fordi vi da ville fått 0 i nevneren. Etter hvert som x nærmer seg 2 fra høyre, blir funksjonsverdien større og større, og grafen går opp. Etter hvert som x nærmer seg 2 fra venstre, får funksjonen en mer og mer negativ verdi, og grafen går nedover.

Grafen har altså en vertikal asymptote x=2.

Grafen krysser y-aksen når x=0.

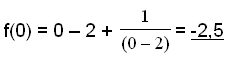
Grafen krysser y-aksen når f(x) = 0. Vi må løse likningen:

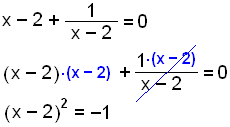Når vi ganger alle ledd med (x-2), får vi en likning uten løsning.

Fordi likningen f(x) = 0 ikke har noen løsning, krysser ikke grafen x-aksen.

Eksemplene ovenfor viser at en rasjonal funksjon nesten alltid har en vertikal asymptote der hvor nevneren er null. (De eneste unntakene er når vi kan faktorisere brøken og bli kvitt nevneren). Funksjonen kan regnes ut for alle andre verdier av x.

Eksempel 5

Først skal vi se på funksjonen

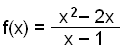
Og finne den vertikale asymptoten og punktene hvor grafen krysser x- og y-aksene.

Først må vi finne ut hvilke x-verdier vi ikke kan regne ut f(x) for. Nevneren er null når x − 1 = 0, dvs. når x = 1.

Den vertikale asymptoten er der hvor x = 1 og funksjonen er gyldig for alle verdier av x, bortsett fra x = 1. Med mengdenotering kan vi skrive

    {xÎR| x ¹ 1} eða R \ {1}

Deretter skal vi finne ut hvor grafen krysser y-aksen ved å regne ut f(0).

    f(0) = (0 − 0)/(0 − 1) = 0

Grafen krysser y-aksen i (0, 0).

For å finne ut hvor grafen krysser x-aksen må vi renge ut likningen     

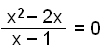x² − 2x = 0∙(x − 1) = 0

x(x − 2) = 0

x = 0 or 2

Grafen krysser x-aksen der hvor x = 0 and x = 2.

Prøv test 4 i funksjoner I.
Husk å fylle inn resultatet i sjekklisten din.