© 2010  Rasmus ehf   og Jóhann Ísak

Funksjoner 2

 Introduksjon 2

Odde og jamne funksjoner. En - til - en - funksjoner og surjeksjoner.

Her er grafene til funksjonene f(x) og g(x).

Definisjonsmengden til f(x) (D_f) er mengden av x - verdier, og verdiområdet (R_f) er mengden av y - verdier. På den venstre grafen er D_f = [1, 5] og R_f = [2, 4] .
På grafen til høyre er  D_g = [1, 3] og R_g = [1, 4].

Grafen til f(x) stiger hele tiden når vi beveger oss mot høyre, og kalles en stigende funksjon.
Grafen til g(x) avtar derimot mot høyre, og er derfor en avtagende funksjon.

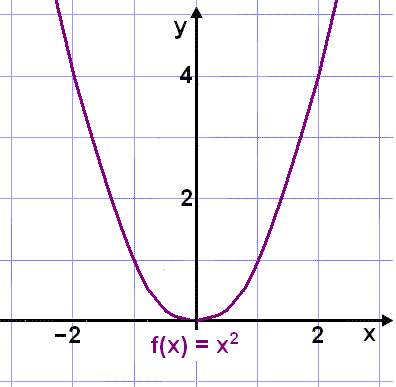
Noen funksjoner kan øke innenfor et intervall, og avta innenfor et annet. Funksjonen f(x) = x² er vist i grafen under. Den avtar i intervallet á¬,0], men stiger i intervallet [0,®ñ.

Funksjonen f(x) = x²

Funksjonen f(x) = x² er en jamn funksjon. Det betyr at Y - aksen, ( x = 0) er symmetriaksen til funksjonen.

Vi kan vanligvis se på grafen om funksjonen er symmetrisk om y - aksen. Vi kan bevise det algebraisk ved å sammenligne f(a) og f(–a).
Hvis  f(–a) = f(a), er f(x) en jamn funksjon.

Eksempel 1

Er   en jamn funksjon?

Kalkulatoren gir en graf som ser slik ut:

For å bevise det, regner vi ut f( -a )

Dette betyr at f(x) er en jamn funksjon.

Eksempel 2

Er f(x) = 8(e^x – x – 1) en jamn funksjon?

Kalkulatoren gir en graf som ligner en parabel.

Med algebra:

   f(–a) = 8(e^–a + a – 1)

     f(a) = 8(e^a – a – 1)

De er ikke like, og funksjonen er derfor ikke jamn.

En funksjon kan også være symmetrisk om origo. Den kan da dreies 180° om punktet (0, 0), og se lik ut som før. Et eksempel på en slik funksjon er  f(x)= x³, og dette kalles en odde funksjon.

Pilene viser at når grafen til f(x) = x³ dreies en halv gang rundt, dekker den samme område som den opprinnelige grafen. For å bevise at en graf er odde, må vi vise at f(–a) = –f(a).

Eksempel 3

Er odde?

Grafen ser slik ut på kalkulatoren.

Vi sammenligner f( a ) med f( -a ) for å være sikker.

Vi ser at f(–a) = –f(a), da må f(x) være odde.

Hvis vi translaterer (flytter) en funksjon som er symmetrisk om y - aksen, vil den alltid få en vertikal symmetriakse. Hvis vi kan skrive en funksjon på formen f(x–a) + b hvor f(x) er symmetrisk om andreaksen, er x = a symmetriaksen.

Hvis vi translaterer en funksjon som er symmetrisk om origo, vil den nye funksjonen være symmetrisk om et punkt.
Skriver vi funksjonen på formen f(x–a) + b hvor f(x) er symmetrisk om origo, er y = f(x–a) + b symmetrisk om punktet (a, b).

Eksempel 4

Er grafen  symmetrisk om et punkt eller en vertikal linje?

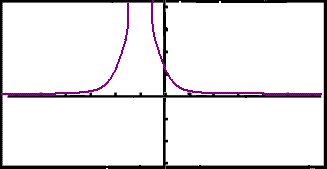
Kalkulatoren gir en graf som ser ut til å bli symmetrisk om en vertikal linje i nærheten av x = –1.

Vi kan skrive om funksjonen slik:

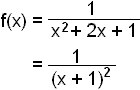
Vi ser av uttrykket at  blir f(x) hvis vi translaterer en enhet til venstre. Nå skal vi undersøke om g(x) er symmetrisk om andreaksen.

g(x) er altså symmetrisk om andreaksen, og vi får f(x) ved å flytte den en enhet til venstre.
Vi kan konkludere med at f(x) har en symmetriakse med likningen x = –1.

Eksempel 5

Er symmetrisk om en linje eller et punkt?

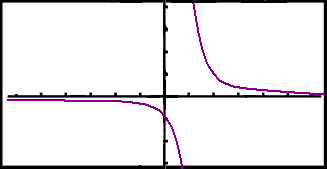
På grafen ser det ut som funksjonen er symmetrisk om et punkt.

Funksjonen tilsvarer translatert en enhet til høyre.

Vi undersøker om g(x) er symmetrisk om origo.

g(x) er symmetrisk om origo (odde), og f(x) er den samme grafen flyttet en enhet til høyre. f(x) er derfor symmetrisk om punktet (1, 0).

Hvis vi har en funksjon f definert for en mengde R, slik at funksjonen kan ha alle verdier i mengden R, kalles funksjonen en surjeksjon for R. Hvis det finnes verdier i mengden R som funksjonen ikke kan ha, er den ikke en surjeksjon.

Eksempel

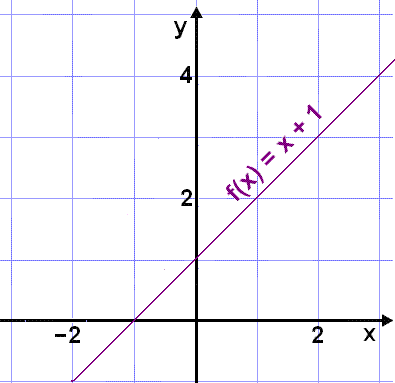
Funksjonen  y = f(x) = x + 1 definert for R har en rettlinjet graf som vist under. Uansett hvilken y - verdi vi velger, kan vi alltid finne en x - verdi som gir y - verdien vi har valgt. Funksjonen f(x) definert som R er en surjeksjon.

f(x) = x + 1
x	F(x)
-2	-1
-1	0
0	1
1	2
2	3
3	4
4	5
5	6
	Alle tall i R kan finnes i denne kolonnen

f(x) = x^{2 er ikke en surjeksjon}. Verditabellen viser at det ikke er noen negative verdier i y - kolonnen.

f(x) = x2
X	f(x)
-2	4
-1	1
0	0
1	1
2	4
	Denne kolonnen kan ikke ha negative verdier

Hvis vi derimot velger mengden R₊ (positive, reelle tall), kan vi finne en x som gir en hvilken som helst y - verdi i mengden R₊. g(x) = x² er derfor en surjeksjon for mengden R₊ .

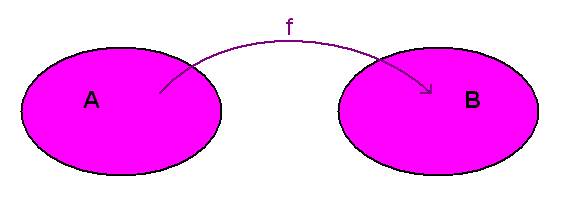
Diagrammet viser forholdet mellom funksjonen f, definisjonsmengden A og kodomenet B. Hvis funksjonen gjelder for ethvert element i mengden B, vil definisjonsmengden A være lik verdiområdet B.

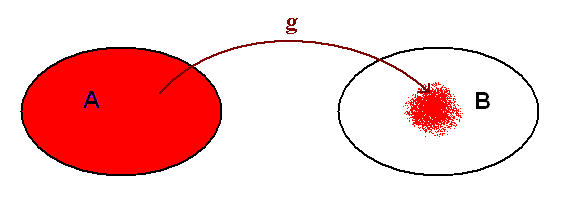
I det neste diagrammet er verdiområdet bare en del av kodomenet B. Det er med andre ord verdier i mengden B som funksjonen ikke kan ha.  

 Nå skal vi se på en annen type funksjoner: en - til - en - funksjoner. I en slik funksjon vil hver x - verdi gi en unik y - verdi. Hvis vi lager en verditabell, vil hver y - verdi altså bare dukke opp en gang. Den formelle definisjonen er slik:

Hvis en funksjon er kontinuerlig og en - til - en, er den enten alltid stigende, eller alltid avtagende. Vi kan lett se dette ved å tegne en horisontal linje gjennom grafen. Hvis linjen bare skjærer grafen en gang, er funksjonen en - til - en. Dette gjelder alle horisontale linjer som kan tegnes gjennom grafen.

Eksempel 6

Er funksjonen  med definisjonsmengden á–2,®ñ en - til - en? 

Hvis funksjonen er en en - til - en - funksjon, gjelder   bare når x₁ = x₂. Dette er åpenbart tilfelle her, så f(x) er en - til - en.

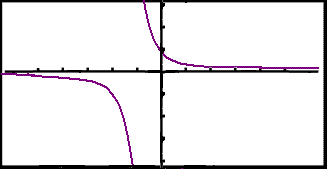
På grafen under ser vi lett at en horisontal linje bare kan skjære grafen en gang. Dette gjelder også utenfor intervallet á–2,®ñ .

Eksempel 7

Er funksjonene f(x) = x² og g(x) = x³ definert i R en - til - en?

 f(–1) = (–1)² = 1 = f(1). To forskjellige x - verdier gir y - verdien 1. Funksjonen er derfor ikke en - til - en. f(x) er en parabel, og en horisontal linje kan skjære den to ganger.

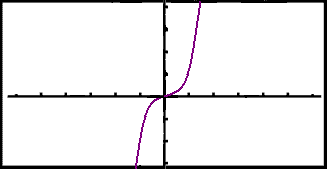
  g(x) = x³ er en - til - en fordi x₁³ = x₂³  medfører at x₁ = x₂ . Grafen vises under, og vi kan lett se at en horisontal linje bare skjærer grafen en gang.

Funksjoner som både er surjeksjoner og en - til - en, kalles bijeksjoner

Funksjonen g(x) = x³ i eksempel  7 er både en surjeksjon og en - til - en. y - verdiene går fra y = –∞ til y = ∞ og funksjonen er økende i hele definisjonsområdet.

Se på eksemplene, og regn deg gjennom test 2 i Funksjoner 2

Husk å fylle ut sjekklisten underveis.