© 2010  Rasmus ehf    og Jóhann Ísak

Funksjoner 2

Introduksjon 4

Funksjonsdrøfting ved derivasjon

Den deriverte av en funksjon er et mål på stigningen til grafen. Vi kan derfor trekke disse konklusjonene:

Dette betyr at når den deriverte bytter fortegn fra pluss til minus, eller minus til pluss, er vi i et stasjonært punkt på grafen. Disse kalles maksimums - og minimumspunkter, selv om de ikke nødvendigvis er de største eller minste verdiene i funksjonen.

Når vi ser på fortegnstabellen til den deriverte, ser vi hvor disse stasjonære punktene oppstår.

En kontinuerlig funksjon kan ikke skifte mellom negative og positive verdier uten å gå gjennom null. Derfor finner vi stasjonære punkter ved å finne ut når den deriverte er 0.

Eksempel 1

Finn den deriverte av  f(x) = x², lag en fortegnstabell, og bruk den til å tegne grafen til f(x).

   Hvis f(x) = x², er f´(x) = 2x.

Vi har et stasjonært punkt når f´(x) = 2x = 0 , altså er x = 0. Tabellen under viser fortegnet til f´(x)

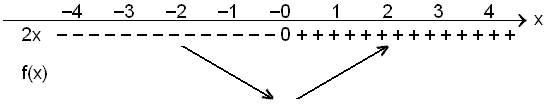
                                 Y = x²

 Den deriverte er 0 når x = 0, så dette er et minimumspunkt.

Eksempel 2

Finn den deriverte av  f(x) = x³ – 3x² + 4, lag en fortegnstabell for den deriverte, og bruk den til å finne de stasjonære punktene. Tegn grafen på en kalkulator, og sammenlign resultatene.

   Hvis f(x) = x³ – 3x² + 4 er f´(x) = 3x² – 6x.

Finn ut hvor den deriverte er 0.

    3x² – 6x = 0

   3x(x – 2) = 0

Likningen har løsningene  x = 0 og x = 2, den deriverte skifter fortegn i disse punktene. Vi finner fortegnet til  f´(x) = 3x² – 6x.

Vi kunne ha lagd tabellen uten å faktorisere først, ved først å velge en x - verdi før, mellom og etter nullene, og deretter finne fortegnet til den deriverte.

   f´(–1) = 3(–1)² – 6(–1) = 3 + 6 = 9    (+)

   f´(1) = 3·1² – 6·1 = –3                       (–)

   f´(3) = 3·3² – 6·3 = 9                         (+)

Dette gir oss en enklere tabell, men med den samme informasjonen.

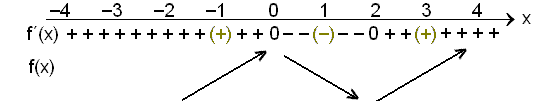
Av tabellen ser vi at det er et maksimumspunkt i x = 0. Stigningstallet er 0, så grafen er horisontal i punktet, og stigningen endres fra positiv til negativ. Den deriverte er også null når x = 2. Her endrer stigningen seg fra negativ til positiv, så dette er et minimumspunkt. Vi kan finne   maksimums - og minimumsverdiene til funksjonen ved å sette disse x - verdiene inn i den opprinnelige funksjonen.

   f(0) = 0³ – 3·0² + 4 = 4

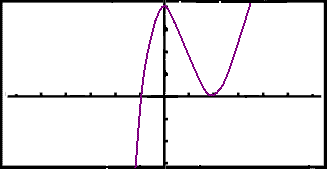
Funksjonen har et maksimumspunkt i  (0, 4).

   f(2) = 2³ – 3·2² + 4 = 8 – 12 + 4 = 0

Funksjonen har et minimumspunkt i (2, 0).

En grafisk kalkulator viser denne grafen:

Noen gang kan den deriverte være null uten å bytte fortegn. I slike tilfeller er det ikke et maksimumspunkt eller minimumspunkt, men et vendepunkt.

Eksempel 3

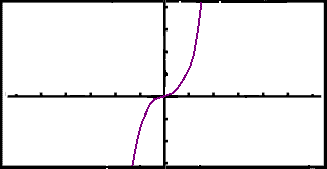
Vi skal undersøke funksjonen f(x) = x³.

Den deriverte er f´(x) = 3x² og er null når x = 0.

Fortegnstabellen til den deriverte:

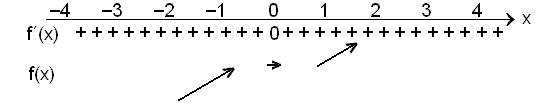
Punktet (0, 0) er et vendepunkt. Grafen øker frem til x = 0, er horisontal i x = 0, og fortsetter å øke etter 0.

Derivasjonsregning har mange praktiske bruksområder, spesielt når vi skal finne maksimums - og minimumsverdier. De neste to eksemplene viser dette.

Eksempel 4

Vi vil lage en pappeske av et kvadratisk stykke papp med sider på 1m. For å gjøre dette, skjærer vi av hjørnene, og bretter som på tegningen. Hvor mye må vi skjære av hjørnene for at esken skal få så stort volum som mulig?

Vi kaller sidene i kvadratene vi skjærer vekk for x. Det betyr at lengden av hver side i esken vil bli 2x kortere enn det opprinnelige kvadratet, altså      1 - 3x. Høyden på esken blir x, og volumet V kan uttrykkes slik:

   V = høyde·lengde·bredde

       = x(1– 2x)(1 – 2x)

       = x(1 – 4x + 4x²)

       = x – 4x² + 4x³

Vi finner ut når den deriverte blir 0:

   V´ = 1 – 8x + 12x² = 0

Dette er en andregradslikning, og vi kan løse den på kalkulator eller med ABC - formelen.

Det sier seg selv at vi ikke kan ha x = ½. Fjerner vi en halvmeter av hvert hjørne, er det ikke noe igjen. Dette gir altså minimumsverdien til volumet. Maksimumsverdien til volumet er altså x = .

   V() = (1 – 2·)(1 – 2·) = m³

Det maksimale volumet til esken vil være m³  når vi skjærer vekk m fra hvert hjørne.

Eksempel 5

Et rektangel er tegnet som vist i diagrammet. Den ene siden bestemmes av linjen y = 3, og det ene hjørnet, P, ligger på grafen til f(x) = x². Finn koordinatene til det punktet P som gir rektangelet det største mulige arealet.

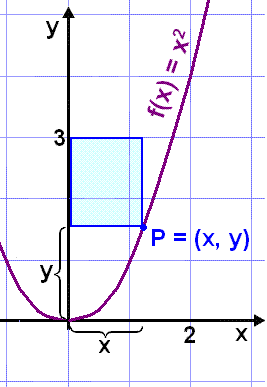
Sidene i rektangelet er x og  3 – y eller 3 – x², fordi punktet P ligger på grafen til f(x) = x². Arealet er derfor:

   A = lengde·bredde

      = x·(3 – x²) = 3x – x³

Vi finner ut hvor den deriverte er null:

   A´ = 3 – 3x² = 0

     3 = 3x²

     x = ±1

Rektangelet er i første kvadrant, så x = –1 kan ikke stemme. Vi får det maksimale arealet når x = 1, så vi setter denne verdien inn i formelen for arealet.

   A = 3x – x³ = 3 – 1 = 2

Se på eksemplene, og regn deg gjennom test 4 i Funksjoner 2.

Husk å fylle ut sjekklisten underveis.