© 2007  Rasmus ehf   og Jóhann Ísak

Mengdelære

Skriv ut

Introduksjon 3  Reelle tall

Vi kan tenke oss tallinjen (x-aksen) som en sammenhengende rekke av punkter. Hvert punkt betegner sin avstand til origo. Vi bruker negativt fortegn (−) hvis punktet er til venstre for origo, og positivt fortegn (+) hvis punktet er til høyre for origo.

Tallmengdene N og Z er ikke de eneste tallene på linjen. De inneholder bare noen få av punktene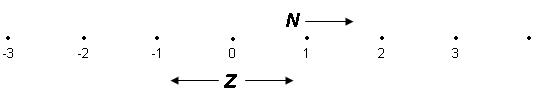

Mengden av rasjonale tall Q finnes også på linjen, men tallinjen inneholder også mange andre tall. Det finnes uendelig mange tall mellom dem vi allerede har nevnt, som ikke kan skrives som brøker, og som derfor ikke er med i mengdene som vi har behandlet.

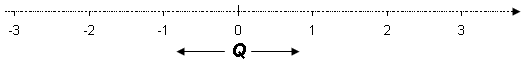
De manglende tallene kalles irrasjonale tall. De har et uendelig antall desimaler etter komma, men desimalene repeterer seg ikke, og er derfor ikke periodiske. Her er noen eksempler:

0,909009000900009
0,123456789101112
	= 1,41421356237
	= 1,73205080756
	= 3,141592653589

De irrasjonale tallene former sammen med Q (som inneholder mengdene Z og N) den sammenhengende tallinjen som vi kaller den reelle tallinjen. Den reelle tallinjen inneholder mengden av reelle tall, R.

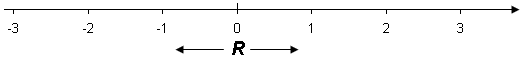
Det følgende diagrammet viser forholdet mellom mengdene R, Q, Z og N. Mengden R inneholder alle de andre mengdene, og kan deles inn i rasjonale tall og irrasjonale tall. Delen av diagrammet som ikke er markert, inneholder de irrasjonale tallene. Delen som er markert av horisontale linjer, viser de rasjonale tallene (mengden Q). Mengden Q kan deles inn i hele tall (mengden Z) og brøker som ikke er hele tall. Til slutt kan Z deles inn i hele, positive tall (mengden N) og negative tall med null

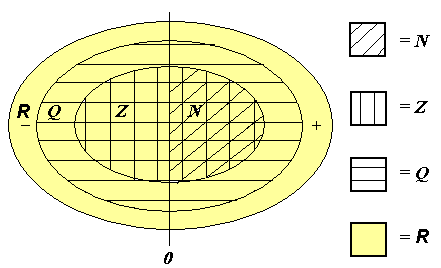
Vi kan beskrive intervaller på den reelle tallinjen på forskjellige måter. For eksempel kan intervallet mellom 1 og 5 inkludert disse, skrives på følgende måte:

Med ulikhet:                 1  x  5

Med mengdenotering:     {  x R | 1  x 5 }

Med diagram:

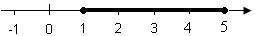
En annen måte er ved å bruke intervallparenteser. Eksempelet ovenfor kan også skrives:

Et intervall som [1,5], hvor begge endene er inkludert, kalles et lukket intervall.

Hvis man vil skrive et uttrykk for et intervall mellom to tall, men som ikke inkluderer endene, skriver man det litt annerledes.

For eksempel tallene som er mindre enn 5, men større enn 1:

Med ulikhet:                         x ≥ 1

Med mengdenotering:       { x R | x ≥ 1 }

Med diagram:    

Med intervallparenteser:

Legg merke til at diagrammet har åpne sirkler, eller hull på endene for å vise at 1 og 5 ikke er med.

Legg også merke til at vi bruker en annen type parenteser for å vise at endene ikke er med.

Intervaller som

hvor ingen av endene er inkludert, kalles åpne intervaller.

Til slutt skal vi se på intervaller hvor bare den ene enden er med:

For eksempel kan vi skrive det slik hvis x er større enn, eller lik 1:

Med ulikhet:             x ≥ 1

Med mengdenotering:     { x R | x ≥ 1 }

Med diagram:

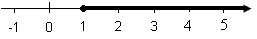
Med intervallparenteser:

Denne typen intervall kalles halvåpen (eller halvlukket). Halvåpne intervaller går ikke alltid uendelig langt på den ene siden.

For eksempel er intervallet

hvor 1 er inkludert, men ikke 5, halvåpen. Her er et diagram som viser intervallet:

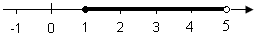
Prøv test 3 i Mengdelære.
Husk å fylle inn resultatet i sjekklisten din.