© 2007 Rasmus ehf og Jóhann Ísak Pétursson
Røtter
© 2007 Rasmus ehf og Jóhann Ísak Pétursson |
Røtter |
|
Introduksjon 1
Kvadratrøtter
Hvis vi regner ut kvadratroten til et tall, og deretter finner kvadratet til resultatet, får vi det første tallet igjen.
| f.eks. |
|
og |
|
Vi kan si at kvadratroten og kvadratet nuller hverandre ut. De er motsatte handlinger.
Hvis vi har et tall opphøyet i andre, er det bare å fjerne totallet når vi skal finne kvadratroten til dette tallet (gjelder bare positive tall).
Et tall som er opphøyet i andre kan derfor fjernes fra under rottegnet ved å fjerne eksponenten 2.
Eksempel 1
Forenkle ved å fjerne den største mulige verdien fra kvadratroten.
a)
 |
Vi begynner ved å faktorisere tallet under rottegnet. Både to og ni dukker opp to ganger. Derfor får vi igjen ett totall og ett nitall når vi tar kvadratroten. I andre eksempel er det bare 9 som dukker opp to ganger, så vi må beholde 3 under rottegnet. |
b)
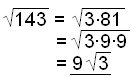
c)
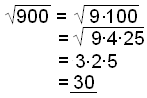
d)
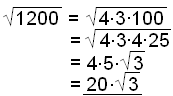
e)

De fleste kvadratrøtter er irrasjonale tall. Det betyr at man ikke kan uttrykke den eksakte verdien deres med brøker eller desimaler.
Derfor får vi unøyaktige verdier når vi bruker kalkulatoren til å finne kvadratrøtter. Hvis vi beholder kvadratroten i svaret, får vi helt nøyaktige svar.
Når vi regner med brøker og kvadratrøtter er det vanlig å ikke beholde noen kvadratrøtter i nevneren.
Å forenkle for å fjerne kvadratrøtter fra nevneren kalles å “Rasjonalisere nevneren”. I de enkleste eksemplene ganger vi bare teller og nevner med kvadratroten som skal fjernes fra nevner.
Eksempel 2
Rasjonaliser nevnerne i disse eksemplene:
a)
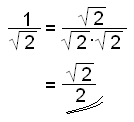 |
Multipliser både teller og nevner med nevneren.Ö 2. Vi får (Ö 2)2 = 2 i nevneren. |
b)
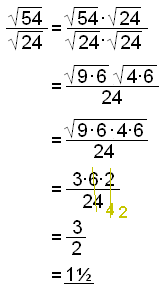 |
Når vi ganger sammen to kvadratrøtter, kan vi sette begge tallene under samme rottegn. |
Det går også an å løse det på denne måten:
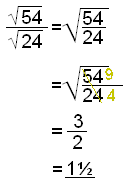 |
Sett hele brøken under et rottegn og forkort. |
Hvis det er to ledd i nevneren, bruker vi denne regelen:
a2 − b2 = (a + b)(a – b)
Vi ganger telleren og nevneren med det motsatte av nevneren, altså det du hadde fått hvis du hadde ganget nevneren med -1.
f.eks. enten med(a − b) eller (a + b).
Eksempel 3
Rasjonaliser nevneren:
a)
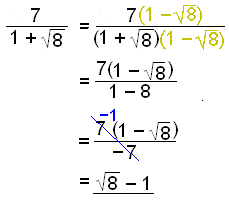 |
|
b)
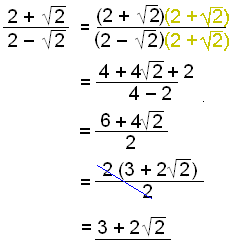
Prøv Quiz 1 i Røtter.
Husk å bruke sjekklisten.