© 2007  Rasmus ehf    og Jóhann Ísak Pétursson

Røtter

Introduksjon 2

Røtter og potenser

Nå skal vi se på forholdet mellom potenser og røtter.

Vi vet at 2∙2 = 22= 4	og derfor
også at 2∙2∙2 = 23 = 8	og derfor
Tretallet foran rottegnet betyr at vi tar tredjeroten.

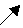Legg merke til at vi ikke skriver 2 når vi tar kvadratroten.

Eksempler:

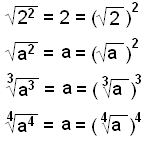
Andre og fjerde eksempel stemmer bare hvis a ikke er negativ.

Røtter og potenser er motsatte operasjoner, som for eksempel multiplikasjon og divisjon (hvis du ganger med et tall, og deretter deler på det samme tallet, er det som om ingenting har skjedd). Vi kan si at de annullerer hverandre.

Likningen (a²)^x = a har bare en mulig løsning: x = ½, altså er å finne kvadratroten det samme som å opphøye i ½.

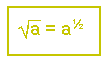	Kvadratroten er det samme som å opphøye i ½.
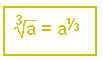	Med tredjerot får vi:

Generelt for alle røtter og potenser:

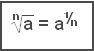
Vi kan gjøre utregningene lettere ved å gjøre røttene til brøkpotenser og bruke potensreglene.

Eksempel 1

Forenkle og gi svaret som en potens:

a)

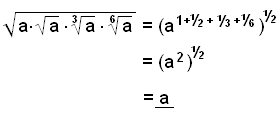Gjør om alle røttene til brøkpotenser og legg dem sammen. Gang deretter med ½.

b)

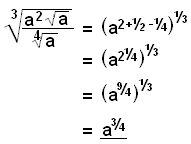
For å løse en likning som

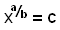
Opphøyer vi begge sider i b/a.

Eksempel 2

Løs likningene:

a)

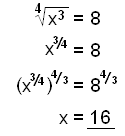Når vi opphøyer begge sider i 4/3, får vi x i første potens.

b)

	her bruker vi potensen

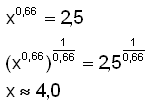Denne metoden er veldig enkel å bruke, men vi må passe på. I noen tilfeller vil nemlig metoden gi feil svar.

Når vi opphøyer i partall, blir alle negative verdier positive, og vi må kontrollere at svarene er riktige ved å sette inn i den originale likningen.

Eksempel 3

Se på dette eksempelet:

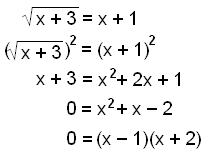
Vi får løsningene x = 1 og x = −2. Nå skal vi kontrollere dem:

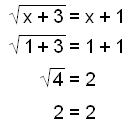
Løsningen x = 1 er riktig.

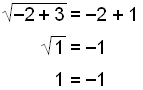
Løsningen x = −2 er gal. Vi mistet minuset på venstre side da vi kvadrerte.

Noen ganger er begge løsninger riktige. Se på det neste eksempelet.

Eksempel 4

Finn x:

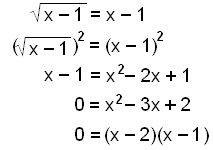
Vi får løsningene x = 1 og x = 2.

Når vi kontrollerer, finner vi ut at

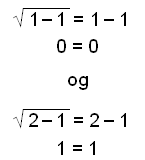
Begge er altså riktige.

Prøv Test 2 i Røtter.  

Husk å bruke sjekklisten.