© 2008 Rasmus ehf og Jóhann Ísak
© 2008 Rasmus ehf og Jóhann Ísak |
Likninger III |
|
Likninger av tredje og fjerde grad
Hvordan kan vi løse tredjegradslikninger som denne?
x3 − x2 – 4x + 4 = 0
Formelen for å løse tredjegradslikninger er veldig komplisert. Noen kalkulatorer har denne formelen innebygd, og kan regne ut slike likninger.
Nå skal vi lære å løse disse likningene ved hjelp av faktorisering. Hvis løsningen består av heltallene a, b og c, kan vi faktorisere likningen slik:
x3 − x2 – 4x + 4 = (x − a)(x − b)(x − c) = 0
Når vi ganger sammen parentesene, ser vi at konstantleddet, 4, er det samme tallet som a, b og c multiplisert sammen.
abc = 4
Alle løsningene a, b og c må være faktorer av 4, så vi har bare disse mulighetene:
±1, ±2 og ±4
Vi kan undersøke hvert enkelt tall for å finne ut hvilke som er løsninger på likningen.
f(1) = 13 − 12 – 4∙1 + 4 = 0 1 er en lösning
f(−1) = (−1)3 − (−1)2 – 4∙(−1) + 4 = 6
f(2) = 23 − 22 – 4∙2 + 4 = 0 2 er en lösning
f(−2) = (−2)3 − (−2)2 – 4∙(−2) + 4 = 0 −2 er en lösning
Nå som vi har funnet tre løsninger, trenger vi ikke å prøve med 4 og −4. En tredjegradsløsning har aldri mer enn tre løsninger.
Disse tallene er verdiene til a, b og c, og vi kan faktorisere likningen.
x3 − x2 – 4x + 4 = (x − 1)(x − 2)(x + 2) = 0
Denne metoden innebærer å finne heltall som er faktorer av konstantleddet, og deretter undersøke om disse heltallene er løsninger på likningen.
Dessverre vil ikke løsningen bestandig være et heltall.
Hvis vi kan finne en heltallsløsning, for eksempel x = a, vet vi på grunn av
rest - teoremen at (x – a) er en faktor i likningen. Vi kan finne
andregradsfaktoren ved divisjon. Så kan vi løse andregradslikningen ved hjelp av
abc-formelen.
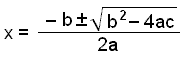
Eksempel 1
Løs likningen x3 − 3x2 – 2x + 4 = 0
Vi setter alle faktorer av 4 inn i likningen for å se om noen av disse er en løsning.
f(1) = 13 − 3∙12 – 2∙1 + 4 = 0 1 er en løsning
f(−1) = (−1)3 − 3∙(−1)2 – 2∙(−1) + 4 = 2
f(2) = 23 − 3∙22 – 2∙2 + 4 = −4
f(−2) = (−2)3 − 3∙(−2)2 – 2∙(−2) + 4 = −12
f(4) = 43 − 3∙42 – 2∙4 + 4 = 12
f(−4) = (−4)3 − 3∙(−4)2 – 2∙(−4) + 4 = −100
Den eneste heltallsløsningen er x = 1. Når vi har funnet en løsning, trenger vi egentlig ikke å sjekke resten av faktorene, fordi vi kan løse likningen ved å dele på (x − 1) og løse andregradslikningen vi får.

Vi kan faktorisere uttrykket slik:
x3 − 3x2 – 2x + 4 = (x − 1)(x2 − 2x − 4) = 0
Det gjenstår å løse likningen
x2 − 2x − 4 = 0
Vi bruker abc-formelen med a = 1, b = −2 og c = −4.

Vi har nå funnet alle løsningene på likningen x3 − 3x2 – 2x + 4 = 0.
x = 1
x = 1 +
![]() 5
5
x = 1 −
![]() 5
5
Eksempel 2
Vi kan også bruke den samme metoden til å løse enkelte likninger av fjerde, eller enda høyere grad. Løs likningen f(x) = x4 − x3 − 5x2 + 3x + 2 = 0.
Først finner vi heltallsfaktorene av konstantleddet, 2. Heltallsfaktorene av 2 er ±1 og ±2.
f(1) = 14 − 13 − 5∙12 + 3∙1 + 2 = 0 1 er en løsning
f(−1) = (−1)4 − (−1)3 − 5∙(−1)2 + 3∙(−1) + 2 = −4
f(2) = 24 − 23 − 5∙22 + 3∙2 + 2 = −4
f(−2) = (−2)4 − (−2)3 − 5∙(−2)2 + 3∙(−2) + 2 = 0 er en løsning
Siden vi har funnet to løsninger, 1 og -
2, kan vi dele på x – 1 og x + 2 uten å få noen rest. Vi gjør dette i to steg:
Først deler vi på x + 2

Vi får en tredjegradslikning, og denne deler vi på x − 1.

Vi har nå faktorisert
f(x) = x4 − x3 − 5x2 + 3x + 2 til
f(x) = (x + 2)(x − 1)(x2 − 2x − 1) Da er det bare å løse andregradslikningen.
x2 − 2x − 1 = 0. Vi bruker formelen, hvor a = 1, b = −2 og c = −1.
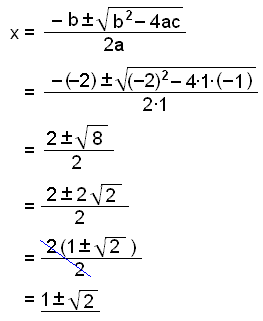
Nå har vi funnet til sammen fire løsninger:
x = 1
x = −2
x = 1 +
![]() 2
2
x = 1 −
![]() 2
2
Noen ganger kan vi løse en tredjegradslikning ved å sette leddene to og to inn i parenteser, og finne en faktor som de har felles.
Eksempel 3
Løs likningen x3 − 2x2 − 4x + 8 = 0
x3 − 2x2 − 4x + 8 = 0 (x3 − 2x2) − (4x − 8) = 0 [x2(x − 2) − 4(x − 2)] = 0 (x − 2)[x2 − 4] = 0 (x − 2)(x − 2)(x + 2) = 0 |
Her kan vi sette (x − 2) utenfor en parentes. |
Merk at parentesen (x − 2) dukker opp to ganger når vi er ferdige med å faktorisere. x = 2 er derfor en dobbel løsning, og vi har bare to forskjellige løsninger:
x = 2 og x = −2.
Til nå har vi bare sett på likninger hvor leddet i den høyeste potensen hadde koeffisienten 1.
Hva kan vi gjøre med likninger hvor koeffisienten er et annet tall?
Den generelle formen er f(x) = ax3 + bx2 + cx + d hvor a, b, c, och d er heltal.
Vi kan se etter heltallsløsninger som før, ved å undersøke om faktorene av konstantleddet er en løsning. Hvis vi finner en heltallsløsning, kan vi dividere, og finne de andre løsningene som før.
Hvis ingen av faktorene av d er en løsning, må vi se
etter parentes -løsninger.
Vi går ut fra at det finnes en parentes - løsning, og vi kaller denne
x =
t/n.
Dette betyr at x − t/n är en faktor av f(x), er en faktor av f(x), eller, hvis vi ganger med n, at xn − t er en faktor.
Når vi har delt f(x) på xn – t, og har funnet andregradsfaktoren, kan vi kalle den.
Ax2 + Bx + C.
Vi har
ax3 + bx2 + cx + d = (xn − t )( Ax2 + Bx + C )
Hvis ser på koeffisientene til
x3 på begge sider av likningen, ser vi at a = nA, og at n må være
en faktor av a.
Vi kan sammenlikne konstantleddene på samme måte, og ser at d = −tC og at t
er en faktor av d.
Enhver parentes som er en løsning av den kvadratiske likningen ax3 + bx2 + cx + d må altså være på formen t/n, hvor t er en faktor av d, og n er en faktor av a.
Generelt for en formel av n’te grad:
f(x) = anxn + an−1xn−1+ ∙ ∙ ∙ ∙ + a1x + a0
med koeffisientene a0, a1, a2, ∙ ∙ ∙ ∙ ∙ an−2, an−1 og an
Hvis funksjonen har en rasjonell løsning, for eksempel t/n, er t en faktor av a0, og n er en faktor av an .
Eksempel 4
Løs likningen f(x) = 2x3 − 7x2 + 4x + 3 = 0.
De mulige heltallsløsningene til f(x) er faktorene til 3, altså ±1 og ±3. Parentesene som kan være røtter er disse fire tallene delt på faktorene til 2. De rasjonelle tallene vi må bruke er ±½, ±1, ±3/2 og ±3.
Vi ser med en gang at vi ikke trenger å ta med noen negative tall, fordi de vil gi negative verdier av f(x), ikke 0.
Her er mulighetene:
f(½) = 2(½)3 − 7(½)2 + 4∙½ + 3 = 3½
f(1) = 2∙13 − 7∙12 + 4∙1 + 3 = 2
f(3/2) = 2(3/2)3 − 7(3/2)2 + 4∙3/2 + 3 = 0 Her har vi funnet en løsning.
x = 3/2 er en løsning, så (x − 3/2) er en faktor. Å dele med (x − 3/2) kan bli vanskelig, så vi ganger isteden med 2 og deler på (2x – 3). Hvis (x − 3/2) er en faktor,
vil også (2x − 3) være en faktor.
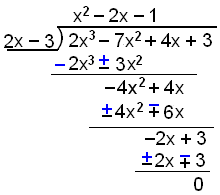
Nå må vi løse
likningen x2 − 2x − 1 = 0. Vi har allerede løst likningen i
eksempel 2. Løsningene var
1 +
![]() 2
og 1 −
2
og 1 −
![]() 2.
2.
De tre løsningene vi har funnet:
x = 3/2 = 1½
x = 1 +
![]() 2
2
x = 1 −
![]() 2
2
Prøv test 2 i likninger III.
Husk å bruke sjekklisten for å få oversikt over hva du har gjort.