© 2008  Rasmus ehf  og Jóhann Ísak

Trekanter

Introduksjon 1

Regler for trekanter

Det er vanlig å merke hjørnene i en trekant med store bokstaver, og sidene med små bokstaver.

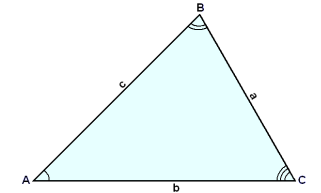
Rett overfor vinkel A, har vi siden a, osv. Se tegningen.

Sidene som samles i A, kalles de hosliggende sidene til A. Den vannrette siden nederst i trekanten kalles grunnlinjen.

Summen av vinklene i en trekant er alltid 180°. Dette kan vi se ved å tegne en rett linje som går gjennom B og er parallell med siden b (se tegning).

Det blir dannet tre nye vinkler med den nye linjen, og disse er like store som A, B og C. De tre vinklene blir til sammen en rett linje, 180°.

Du har allerede lært at arealet av en trekant er gitt ved formelen

                                               Areal  F = ½∙b∙h

G er skjæringspunktet mellom grunnlinjen og høyden. Dette punktet kalles ofte normalen fra punktet B på linjen b.

To trekanter er formlike hvis de har de samme vinklene. For å vise at to trekanter er formlike, holder det å vise at to av vinklene er like, fordi den tredje vinkelen da også må være lik i de to trekantene.

Trekantene i tegningen over er formlike. Da må også forholdet mellom de korresponderende sidene være det samme.
Det vil si at:

og

Nå skal vi bruke disse forholdene til å løse noen oppgaver.

Eksempel 1

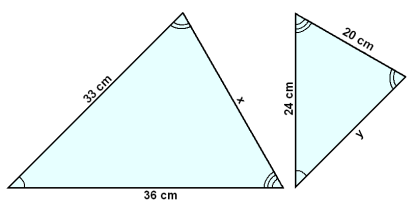
Trekantene i tegningen er formlike, og de korresponderende vinklene er markert på samme måte. Vi skal regne ut sidene x og y.

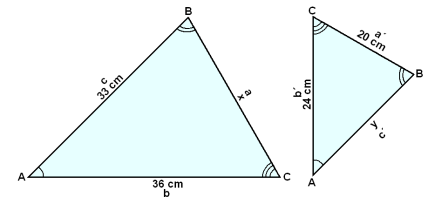
Vi har disse forholdene:

    ^b/_c = ³⁶/₃₃ = ²⁴/_y = ^b´/_c´

Det betyr at ^y/₂₄ = ³³/₃₆ og at  y = ^24∙33/₃₆ = 22 cm.

Vi får også at  ^a/_b = ^x/₃₆ = ²⁰/₂₄ = ^a´/_b´

Vi finner at x = ^36∙20/₂₄ = 30 cm.

Ved å bruke forhold mellom sidene, kan vi komme frem til en annen regel for trekanter.

Vi tegner en rett linje mellom to av sidene, som er parallell med den siste siden. Trekanten blir delt inn i to deler, og den øverste delen er en mindre trekant som er formlik med trekant ABC. Vi merker sidene i den lille trekanten med x, y og z.

Linjen deler c inn i to deler, x og r. a deles inn i z og t. Vi setter inn x + r for c og z + t for a i likningen over:

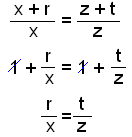
Vi har vist at forholdet mellom de to delene av hver linje blir likt, når man trekker en linje som går mellom to av sidene i en trekant, og er parallell med den siste.

Eksempel 2

To av sidene i trekanten ABC, AB og BC, er 30 cm lange. Grunnlinjen, AC, er 42 cm. Vi trekker en linje fra punktet X på AB, som er parallell med grunnlinjen og 14 cm lang fra AB til BC. Finn BX og AX.

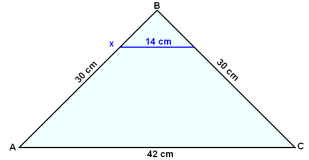
    ¹⁴/₄₂ = ^XB/₃₀

        XB = ^30∙14/₄₂ = 10 cm

   AX = 30 − 10 = 20 cm

For å finne vinklene kan vi enten tegne en nøyaktig tegning og måle, eller bruke trigonometri.

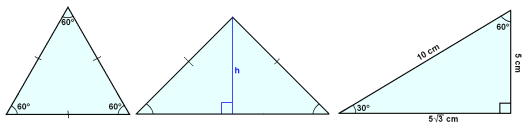
     Likesidet.                     Likebent.                    Rettvinklet.

I en likesidet trekant er alle sidene like lange, og alle vinklene er 60°.

I en rettvinklet trekant gjelder Pythagoras regel: a² + b² = c²

Vi kan forsikre oss om at den tredje trekanten i tegningen over er rettvinklet ved å bruke Pythagoras:

    5² + (5)² = 10²

            ^{25 + 75 = 100}

Legg merke til at hypotenusen (10 cm) er dobbelt så lang som den korteste kateten (5 cm).
Da må dette være en ”30, 60, 90 – trekant”, med vinklene 30°, 60° og 90°.

Eksempel 3

Finn arealet av en likesidet trekant hvor sidene er 10 cm.

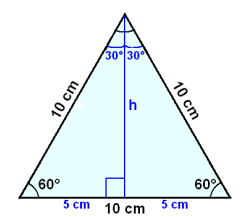
Vi begynner med å tegne inn høyden h. Dette deler inn trekanten i to like, rettlinjede trekanter. Vi regner ut h ved hjelp av Pythagoras.

   h² + 5² = 10²

           h² = 10² − 5² = 100 − 25 = 75 = 5²∙3

            h = 5 ≈ 8,7

 Areal A = ½∙10∙h ≈ ½∙10∙8,7 ≈ 43 cm²

Eksempel 4

I en likebenet trekant er sidene 42 cm, 30 cm og 30 cm. Finn lengden av en linje som går mellom de to like sidene, er parallell med grunnlinjen og er 10 cm fra grunnlinjen.

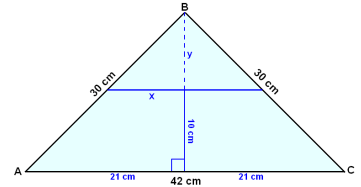
Først tegner vi inn h, og deler trekanten inn i to rettlinjede trekanter. Så bruker vi Pythagoras til å regne ut høyden.

   h² + 21² = 30²

            h² = 30² − 21² = 459

            h ≈ 21,4

         y = h − 10 ≈ 21,4 − 10 ≈ 11,4 cm

   Ved å bruke forholdsregelen får vi:   

    ^y/_h = ^x/ ₂₁

       x ≈ ^21∙11,4/ _21,4 ≈ 11 cm

Derfor er lengden av linjen 22 cm.

Vi tegner den rettvinklede trekanten ved å bruke hypotenusen AB som grunnlinje, slik at den øverste vinkelen C er 90°. Vi tegner høyden fra C ned på AB.

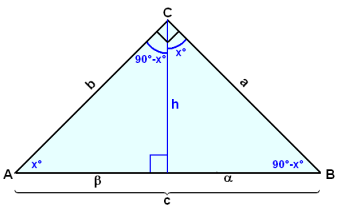
Linjen deler vinkel C i to nye vinkler (ikke like hvis ikke trekanten er likebent). Hvis den ene delen er X°, må den andre være 90° - X°. Da blir vinklene ved grunnlinjen 90° − x° på høyre side, og x° på venstre side, fordi summen alltid er 180°.

Merk at alle vinklene i både de små trekantene, og også i den opprinnelige trekanten ABC, er like, nemlig 90°, x° og 90 - x°. De tre trekantene er derfor formlike.

Denne regelen gjelder alle rettvinklede trekanter:

Linjen fra den rette vinkelen normalt på hypotenusen deler alltid en rettvinklet trekant inn i to nye trekanter, som begge er formlike med den første trekanten.

Fra dette kan vi sette opp tre forhold.

Vi bruker greske bokstaver. står for står for siden rett overfor vinkelen x°, og står for vinkelen rett overfor vinkelen 90°− x°.

Fordi de to små trekantene er formlike, er

Fordi de to små trekantene er formlike, er

Den opprinnelige trekanten og trekanten med toppvinkel 90° - x° er formlike, og

Eksempel 5

Vi har en rettvinklet trekant med katetene 7 cm og 10 cm. Normalen fra den rette vinkelen ned på hypotenusen deler trekanten inn i to nye trekanter. Finn arealet av disse trekantene.

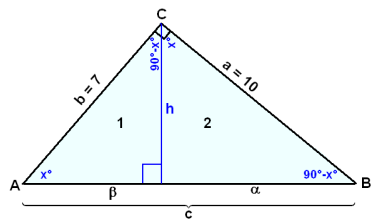
Først finner vi hypotenusen c ved hjelp av Pythagoras:

    c² = 10² + 7² = 149,  Da blir  c ≈ 12,2 cm

Deretter bruker vi forholdet mellom sidene til å finne .

    ^a/_c = /_a

    = a²/_c ≈ 10²/_12,2 ≈ 8,2 cm

Deretter finner vi .

    ≈ 12,2 − 8,2 ≈ 4 cm

Så må vi finne høyden h.

    ^b/_c = ^h/_a

    h = ^ab/_c ≈ ^10∙7/_12,2 ≈ 5,7 cm

Nå er det lett å regne ut arealene:

    Areal  F₁ = ½∙∙h ≈ ½∙4∙5,7 ≈ 11,4 cm² 

    Areal  F₂ = ½∙∙h ≈ ½∙8,2∙5,7 ≈ 23,4 cm² 

Prøv Test 1 i Trekanter.  

Husk å bruke sjekklisten.