| © 2006 Rasmus ehf |
Introduksjon 6.
Dersom du har penger i en bank, så betaler banken rente til deg. Renten er en slags leie som banken betaler til deg for å få disponere sparepengene dine. Hvor mange kroner du får i rente, kommer an på prosenten, eller rentefoten og hvor mye du sparer. Renten beregnes som en del av det hele, kapitalen, som i prosentregning.
Om du har 150.000 kr på din konto i banken i ett helt år og rentefoten er 12% pa. ( Pa. betyr per annum = per år ), så kan du beregne renten med vanlig prosentregning.
Dvs. Rentefot multiplisert med kapitalen = renten
Rentefoten kan gjøres om til desimaltall: 12% = 12/100 = 0,12
![]()
På ett år får du 18000 kr i rente.
Om du har 150.000 kr på din bankkonto i 6 måneder eller et halvt år, får du
| I rente på et halvt år |
Tiden (t) kan tas med i prosentligningen, og renten kan regnes ut.
rentefot·kapital·tid = rente
| eller | i rente på et halvt år. |
| Eller et halvt år |
Dersom kapitalen er i banken i 3 måneder, regner du slik:
rentefot·kapital·tid = rente
3måneder = 3/12 år = 0,25 år Da er tid 0,25
eller 4500 kr i rente på 3 måneder.
Vi regner med 30 dager i en måned og året blir derfor 12 x 30 dager eller 360 dager.
150000 kr står i banken fra 26. august til 8. november samme år. Rentefoten er 12% pa. Vi må først regne ut antall dager pengene står i banken, rentedager, før vi kan beregne renten for denne perioden
| Antall rentedager: | ||
| perioder | dager | |
| august (30-26) | 4 | |
| sept. | 30 | |
| okt. | 30 | |
| nov. | 8 | |
| Totalt: | 72 | |
72 dager av 360 er 72/360 år = 0.2 år. Du får
![]()
Uttaket i november blir: kapitalen, 150000 kr + renten, 3600 kr = 153600 kr.
Renten av 150000 kr ble 4500 kr etter tre måneder i banken. Finn rentefoten!
Obs tre måneder er 3 av 12 = 3/12 år = 0.25 år
| Prosent·kapital·tid = rente | Renteligningen |
| Setter inn de oppgitte verdiene og kaller rentefoten p (ukjent) | |
| Multipliserer kapital og tid | |
| Dividerer med tallet som står ved p og skriver på desimalform og gjør om til prosent. |
Vi ser at rentefoten er 12 %.
Renten av en kapital på150000 kr var 7200 kr og rentefoten var 12%
Regn ut hvor lenge denne kapitalen var i banken.
| Prosent·kapital·tid = rente | Renteligningen |
| Setter inn gitte verdier for kapital og rentefot og kaller tiden for t (ukjent) | |
| Multipliserer sammen kapital og rentefot. | |
| Dividerer med tallet som står ved t og skriver på desimalform. | |
| Multipliserer med antall dager i året. |
Vi ser at kapitalen var i banken i 144 dager.
Vi tar 164400 kr ut av banken. Kapitalen har stått i banken i 288 dager og rentefoten er 12%. Vi vet ikke hvor mye som ble satt inn i banken og heller ikke renten.
Obs. 288 dager av 360 er 288/360 = 0.8 år.
0,12·kapital·0,8 = rente
| Prosent·kapital·tid = rente | Renteligningen |
| 0,12·kapital·0,8 = rente | Sett inn de gitte verdier for rentefot og tid |
| kapital+0,12·kapital·0,8 = rente+kapital | Legg til kapitalen på begge sider av likhetstegnet |
|
kapital +
0,096kapital =
164400kr 1K + 0,096K = 164400kr |
Multipliserer 0.12 og 0.8 og setter inn den gitte verdien, uttaksbeløpet = rente +kapital. Kaller kapitalen for K(ukjent) |
| 1,096K = 164400kr | 1K + 0.096K = 1.096K |
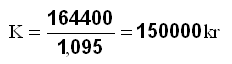 |
Dividerer med tallet som står ved K og da finner du 1K som er kapitalen. |
150000 kr ble satt inn i banken.
Vi har 150000 kr i banken i 5 år. For å finne ut hvor mye vi kan ta ut når rentefot er 12 %, skal vi først se litt på hva som skjer år for år.
| og 150000 kr + 18000 kr = 168000 kr. | |
| 168000 er 112% av 150000. |
For hvert år som går blir kapitalen endret.
| 1 år | ||
| 2 år | ||
| 3 år |
Om vi fortsetter med 12% rentefot får vi:
| Kapital etter 3 år | ||
| Kapital etter 5 år |
Kapital og rente etter 5 år er da
![]()
| Kapital og rente etter x år er da |
|
Her er:
|
K = kapital og rente etter x år |
|
k = kapital som ble satt i banken |
|
p = rentefoten skrevet på desimalform |
|
x = år |
Gjør nå test 6 i prosentregning