© 2006  Rasmus ehf

Statistikk

Print

Introduksjon 4.

•  Histogram og Frekvens

• Tilfeldig utvalg

• Gjennomsnitt

Frekvens

Her skal vi se på fordelingen av vekten til 30 elever på 10. trinn. Vi sorterer målingene i stigende rekkefølge: (målt i kilo)

 50, 52, 54, 55, 57, 57, 58, 60, 60, 60, 61, 61, 62, 62, 63, 64, 65, 66, 66, 67, 67, 67, 67, 68, 70, 70, 71, 72, 73, 74

Ofte samler vi målingene i grupper, intervaller. Vi velger en intervallbredde på 5 kg.

 Histogram   Fordelingen kan så vises i et histogram

Dette histogrammet viser fordelingen av 30 elevers vekt.

Siden ingen i gruppen var lettere enn 50 kg tas ikke den del av aksen med. Dette vises med en brutt linje. Histogram har stolper som ligger tett sammen og har lik bredde.  Av histogrammet kan vi se at 3 av disse 30 er 50 - 54 kg, altså 10 % av gruppen.

Tilfeldig utvalg:

Dersom store mengder informasjon skal undersøkes, er det lurt å bruke statistikk. Nå skal vi undersøke tilgangen til Internett hos elever i 10. klasse i en by. Det er totalt 4500 10. klassinger, så det vil ta veldig lang tid å spørre alle sammen. Vi snakker med 100 elever, som er valgt tilfeldig, altså et tilfeldig utvalg.

Vi passer bare på at det er like mange gutter som jenter, altså 50 gutter og 50 jenter.

Vi har følgende spørsmål.:

• Har du tilgang til Internett hjemme?  

• Har du egen pc som er oppkoplet til Internett?

Resultatet er følgende.

Utvalget er 100 elever, så det er enkelt å skrive resultatet i prosent.

Vi ser at 85 eller 85 % av elevene i utvalget har tilgang til Internett og da kan vi forutsi noe om det totale antall elever i 10. klasse som har tilgang til Internett. Basert på utvalget er det 85 % av elevene. Vi regner derfor 85 % av 4500 og får at 0.85 x 4500 = 3825 .

 Derfor kan vi si med relativ sikkerhet at over 3800 elever i 10. klasse har tilgang til Internett hjemme.

Lignende metoder brukes ved forskjellige meningsmålinger og brukerundersøkelser:

Eksempler:

• Valgprognoser
• Seertall
• Avislesere

Utregning av gjennomsnitt:

På en skole i Island deltok de to 10. klassene i nasjonale prøver i matematikk og resultatet var følgende

Klasse A : gjennomsnittskarakter: 7,0    Antall elever var 20

Klasse B: gjennomsnittskarakter 6,0    Antall elever var 30

Vi skal nå regne skolens gjennomsnittskarakter

Vi kan ikke addere klassenes gjennomsnittskarakterer eller 7+ 6= 13 og så dividere med 2 og påstå skolens gjennomsnittskarakter er 6,5, fordi det er ikke like mange elever i de to klassene.

Gjennomsnitt:

Vi må addere alle elevenes karakterer i begge klassene og dividere den summen med det totale antall elever i begge klassene.

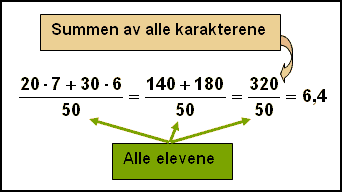
Vi regner ut gjennomsnittet på skolen ved å addere alla karakterene og dividere med antall elever. Gjennomsnittskarakteren er 6,4, ikke 6,5

Øv på dette og gjør så test 4 i Statistikk.
Obs !  Husk å fylle ut sjekklisten.