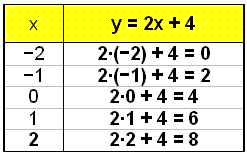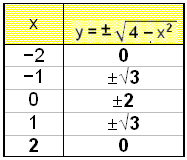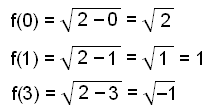|
© 2009 Rasmus ehf og Jóhann Ísak |
Funkcje I |
Drukuj |
Prezentacja nr 1
Funkcje i wykresy
Przyjrzyjmy się kilku prostym równaniom, które wskazują związek dwóch zmiennych, x i y, i określmy jakim punktom w układzie współrzędnych one odpowiadają.
Dla x wybieramy wartości -2, -1,
0, 1 i 2, obliczamy dla nich wartość y i umieszczamy w tak zwanej tabeli wartości.
Przykład
nr 1
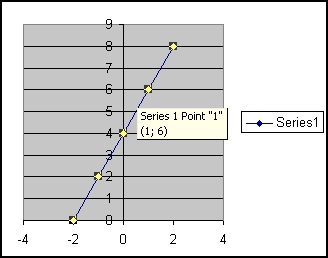
Mamy równanie y=2x + 4.
Najpierw tworzymy
tabelę obliczonych wartości y dla wybranych przez nas wartości
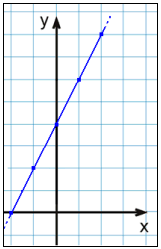
x. Gdy narysujemy te punkty w układzie współrzędnych to
widzimy, że leżą one na linii prostej. Łączymy razem
punkty.
|
|
|
Bardzo prosto robi się to przy użyciu kalkulatora. Jeśli mamy kalkulator Casio to z Menu wybieramy opcję TABLE.


Potem wpisujemy funkcję 2x+4 w polu Table Func (Y1 = 2x + 4), które jest teraz na ekranie.
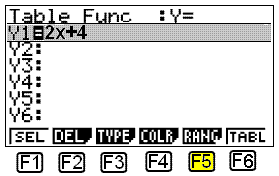
Teraz musimy się zdecydować jakie wartości x chcemy użyć. Aby to zrobić wybieramy opcje RANGE poprzez naciśnięcie guzika F5. Pojawi się ekran:
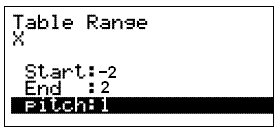
Wybieramy początek (start) -2 i koniec (end) 2. Pitch mówi nam o jaką wartość zmienia się x. W naszym wypadku pozostawimy wartość 1 i naciśniemy EXE.
Naciskamy więc klawisze w następującej kolejności:
![]()
Zabierze nas to z powrotem do poprzedniego ekranu gdzie wybieramy TABLE przez naciśnięcie F6. Teraz na ekranie pojawi się tabela wartości.
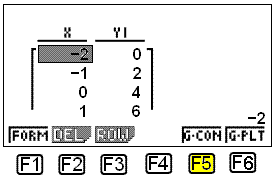
Możemy narysować wykres wybierając G-CON (F5).
Możliwe jest też stworzenie tabeli wartości oraz wykresu w
programie EXCEL ![]()
Uruchom program Excel i wykonaj
następujące doświadczenia:
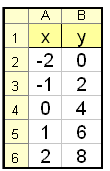
W programie EXCEL wprowadzamy liczby -2 i -1 w komórki A2 i
A3 (spójrz na tabelę EXCEL'a powyżej), a resztę kolumny A możemy teraz wypełnić
automatycznie przez zaznaczenie komórek A2 oraz A3 i następnie skopiowanie
w dół. Formuła w B2 jest następująca: =2*A2 + 4 i jest również skopiowana w dół.
|
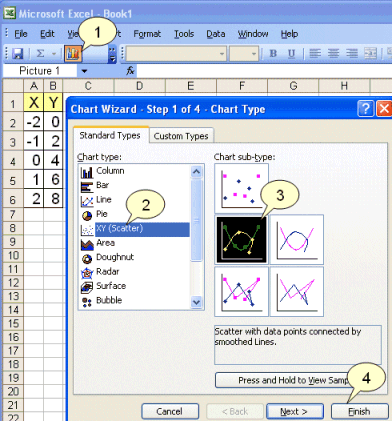
Możemy narysować wykres przez zaznaczenie liczb w dwóch kolumnach, a następnie naciśnięcie przycisku tworzenia wykresów (1). |
|
|
|
Wybieramy „xy-scatter“ (2). |
|
Następnie wybieramy jeden z rodzajów wykresów (3) |
|
|
przed zakończeniem tworzenia wykresu (4). |
Teraz możemy zmieniać wygląd wykresu poprzez zaznaczanie elementu, który chcemy zmienić, a następne naciśnięcie prawego przycisku myszki.
Przyjrzyjmy się kolejnym
przykładom.
Przykład nr 2
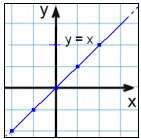
Stwórz tabele wartości i narysuj wykresy następujących funkcji:
|
y = x |
|
|
|
x |
y = x |
|
|
-2 |
-2 |
|
|
-1 |
-1 |
|
|
0 |
0 |
|
|
1 |
1 |
|
|
2 |
2 |
|
|
|
|
|
|
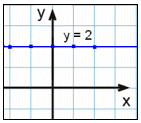
y = 2 |
|
|
|
x |
y = 2 |
|
|
-2 |
2 |
|
|
-1 |
2 |
|
|
0 |
2 |
|
|
1 |
2 |
|
|
2 |
2 |
|
|
|
|
|
|
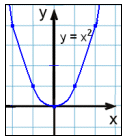
y = x2 |
|
|
|
x |
y = x2 |
|
|
-2 |
4 |
|
|
-1 |
1 |
|
|
0 |
0 |
|
|
1 |
1 |
|
|
2 |
4 |
|
|
|
|
|
|
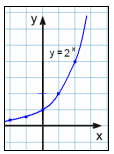
y = 2x |
|
|
|
x |
y = 2x |
|
|
-2 |
1/4 |
|
|
-1 |
1/2 |
|
|
0 |
1 |
|
|
1 |
2 |
|
|
2 |
4 |
|
Teraz przyjrzymy się bliżej kilku przykładom, które mogą być rozwiązane w ten sam sposób. W tych przykładach formuła nie jest napisana jako y= ... i przez to nie możemy użyć "table func." w naszym kalkulatorze.
Przykład nr 3
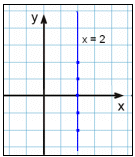
x = 2
Jeśli
jedynym warunkiem jest, żeby x miało wartość 2, to nie ma
znaczenia, jaką wartość ma y. Możemy wybrać
wartości -2,-1,0,1 i 2 i stworzyć następującą
tabelę wartości:
|
|
|
Wynikiem jest pionowa linia przecinająca oś x w punkcie 2.
Przykład
nr 4
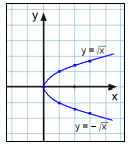
Teraz przestudiujmy zależność y2 = x.
Jeśli rozwiążemy równanie na y to otrzymamy dwa rozwiązania.
y = ±![]()
Innymi słowy są dwie wartości
y dla każdego x, które wybraliśmy. Jesteśmy również
ograniczeni do wyboru jedynie dodatnich wartości x
ponieważ nie możemy brać pierwiastka kwadratowego z
liczby ujemnej. Poniżej możesz zobaczyć tabelę
wartości oraz wykres.
|
|
|
Przykład
nr 5
Teraz przyjrzyj się równaniu x2 + y2 = 4.
Rozwiązując na y:
x2 + y2 = 4
y2 = 4 − x2
![]()
Znów
otrzymujemy dwie wartości y dla każdej wartości x, którą
wybraliśmy. Zauważamy również, że nie możemy
wybrać żadnej wartości x spoza przedziału [-2,2] ponieważ
mielibyśmy liczbę ujemną pod pierwiastkiem. Tabela wartości
oraz wykres są przedstawione poniżej.
|
|
|
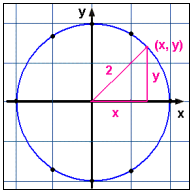
Kiedy rysujemy punkty to widzimy, że wszystkie leżą na okręgu ze środkiem w początku układu współrzędnych (0,0). Promień okręgu wynosi 2 jednostki.
Ten wynik jest łatwy do zrozumienia gdyż x2 + y2 = 4 to właściwie twierdzenie Pitagorasa dla trójkąta prostokątnego o przeciwprostokątnej długości 2 i o przyprostokątnych długości x i y. ( Punkty o współrzędnych (x,y) spełniające równanie muszą znajdować się w odległości 2 od środka układu współrzędnych i tworzą okrąg o promieniu 2.)
Te przykłady wskazują na pewną różnicę jakościową. Jeśli mamy jeden konkretny związek między x a y, np. formułę, która przyjmuje jedną wartość y dla każdej wartości x, to możemy stworzyć prostą tabelę wartości i narysować wykres bez większych problemów. Równania, które łączą jeden y z jednym x są bardzo ważne w nauce i nazywają się funkcjami. Mówimy, że "y jest funkcją x" i zapisujemy to jako y = f(x). Czytamy to "y równa się f od x".
Relacja przyporządkowująca każdej wartości x z dziedziny dokładnie jedną wartość y ze przeciwdziedziny nazywana jest funkcją.
Kiedy patrzymy na wykresy równań, które są funkcjami, to widzimy, że pionowe linie nigdy nie przecinają wykresu więcej niż raz.
Dostrzeżemy to jeśli spojrzymy na wykresy w przykładach, które właśnie przerobiliśmy.

Czerwona pionowa linia przecina wykres 2, 3 oraz 4 w dwóch lub więcej miejscach pokazując, że nie są wykresami funkcji. W przykładzie nr 1 wszystkie pionowe linie przecinają wykres tylko raz. To jest wykres funkcji o równaniu y = x2 .
Funkcje w rodzaju y = x2 są często oznaczane inaczej. Równanie y = x2 możemy zapisać jako f(x) = x2 gdzie y = f(x). Używamy f(x) zamiast y by pokazać, że wartość y zależy od wartości x "jest funkcją x". W tym przypadku, jeśli wybierzemy x = 2 to możemy obliczyć y ze wzoru y = 22 = 4. W języku funkcji powiemy, że f od 2 równa się 4. Możemy zapisać w postaci funkcji f(2) = 22 = 4.
Przykład
nr 6
|
Dana jest funkcja
|
|
|
|
Wstawiamy wartości 0,1 oraz 3 do równania zamiast x i obliczamy wartość funkcji (wartość y) w każdym przypadku. |
|
Dla x=3 rozwiązanie nie istnieje, bo pod pierwiastkiem nie może być liczby ujemnej. |
|
Do funkcji możemy wstawić również litery zamiast liczb. Jeśli f(x) = x3 + x2 to:
f(a) = a3 + a2 i f(a2) = a6 + a4 i f(a+1) = (a+1)3 + (a+1)2.
Przykład
nr 7
Dana jest funkcja f(x) = x2, znajdź f(a), f(2a), f(a+1) i f(a+b).
f(a) = a2
f(2a) =
4a2
f(a+1) =
(a+1)2 = a2 + 2a + 1
f(a+b) = (a+b)2 = a2 + 2ab + b2
Przećwicz powyższe przykłady,
a potem zrób test nr 1.
PS Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.