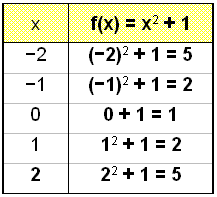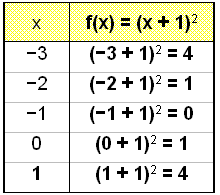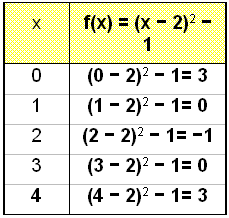|
© 2009 Rasmus ehf og Jóhann Ķsak |
Funkcje I |
Prezentacja nr 3
Funkcje stopnia drugiego
Przyjrzyjmy się ponownie wielomianom stopnia drugiego. Najprostszą postacią funkcji kwadratowej jest f(x) = x2, której wykresem jest parabola.
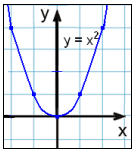
Zauważ, że wykres jest symetryczny względem osi y. Oś y jest nazywana osią symetrii tej funkcji. Teraz przyjrzymy się jak współczynniki wpływają na wygląd wykresu.
Współczynnik stojący przy x2 jest zazwyczaj oznaczany a. Jeśli spojrzymy na różne parabole o różnych wartościach a, to zauważymy, że niektóre z nich są szersze, a inne węższe niż podstawowa parabola o współczynniku a = 1. Tutaj są wykresy parabol o współczynnikach a = 4, 2, ½ i ¼.
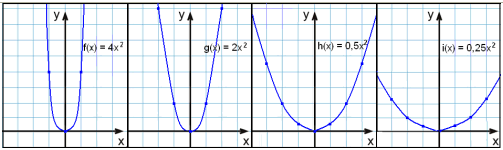
a = 4 a = 2 a = ½ a = ¼
Tutaj widzisz parabole o ujemnych wartościach współczynnika a.
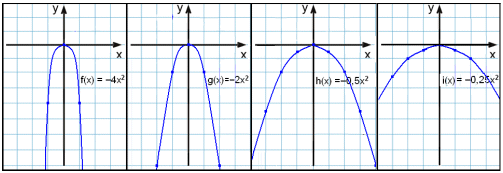
a = −4 a = −2 a = −½ a = −¼
Przy wykresach w rodzaju y = ax2 , jeśli wartość a jest dodatnia to wykres jest wygięty do góry (jak uśmiech). Czym większa wartość współczynnika a, tym węższy jest wykres. Gdy a maleje to wykres staje się bardziej płaski, aż a osiągnie wartości ujemne i zaczyna być wygięty w dół.
Przykład
nr 1
Teraz narysujemy wykres
f(x) = x2
+ 1 i porównamy go z g(x)
= x2.
|
|
|
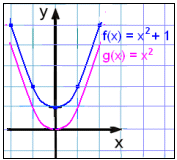
Wartości jakie przyjmuje funkcja w tabeli dla f(x) = x2 +1 są o jeden większe od odpowiadających im wartości w tabeli dla g(x) = x2 i wykres jest przesunięty pionowo o 1.
Zauważ, że wykres f(x) = x2 + 1 nie przecina osi x. Wynika stąd, że równanie x2 + 1 = 0 nie ma rozwiązania. Już to wiemy, ponieważ jakakolwiek liczba podniesiona do kwadratu nie będzie ujemna, zatem x2 nigdy nie będzie równy -1.
Przykład
nr 2
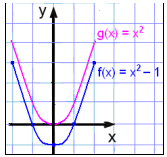
Narysuj wykres funkcji f(x) = x2 − 1 i porównaj go z g(x) = x2.
|
|
|
Teraz wartości funkcji w tabeli f(x) są o jeden mniejsze od odpowiadających im wartościom w tabeli dla g(x) = x2 i wykres przesunął się w dół o 1.
x2 − 1 = 0
Zauważ, że wykres f(x) = x2 − 1 w tym przykładzie przecina oś x w dwóch miejscach. Oznacza to, że równanie x2 − 1 = 0 ma dwa rozwiązania,
x2 = 1
x = ±1
którymi są: x = −1 i x = 1.
Przykład
nr 3
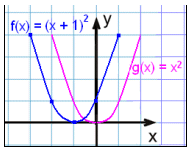
Przyjrzyjmy się
teraz wykresowi funkcji f(x) = (x + 1)2 (lub f(x) = x2 + 2x + 1) i porównajmy go z wykresem g(x) = x2.
|
|
|
Tutaj dodaliśmy 1 do x i możemy zobaczyć, że wszystkie wartości funkcji w tabeli podniosły się o jeden wiersz w porównaniu z tabelą wartości podstawowej funkcji.
Wykres f(x) jest taki sam jak wykres g(x) = x2 tylko przesunięty o 1 w lewo. Mówimy, że wykres podstawowej funkcji został przesunięty o -1 w poziomie. Oś symetrii przechodzi przez x=-1.
Przykład
nr 4
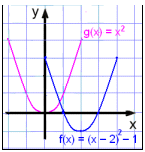
Narysuj wykres f(x) = (x − 2)2 − 1 (lub f(x) =
x2 − 4x + 3) i porównaj go z wykresem funkcji g(x) = x2.
Jeśli zastosujemy tę samą metodę jak w poprzednim przykładzie,
to możemy zgadnąć, że wykres przesunął się o
dwie jednostki w prawo i jedną w dół. Teraz sprawdzimy to
tworząc tabele wartości, zaczynając od x=0 i rysując
wykres.
|
|
|
Zauważ, że oś symetrii przechodzi przez x=2. Możemy znaleźć miejsce przecięcia wykresu osi y bez jego rysowania. Robimy to obliczając f(0) = 3 lub wymnażając nawias i zauważając, że wyraz wolny (wyraz bez x) jest równy 3.
f(x) = (x − 2)2 − 1 = x2 − 4x + 4 − 1 = x2 − 4x + 3
lub f(0) = (x − 2)2 − 1 = 4 − 1 = 3
Przykład
nr 5
Znajdź miejsce
przecięcia wykresu f(x) = (x − 2)2 − 1 z osią x.
Wstawiamy y = f(x) = 0 i rozwiązujemy równanie na x.
|
(x − 2)2 − 1 = 0 |
Najpierw przenieś -1 na drugą stronę równania. |
|
(x − 2)2 = 1 |
Następnie spierwiastkuj obie strony równania. Pamiętaj o + i -. |
|
x − 2 = ±Ö1 = ±1 |
Na końcu przenieś 2 na drugą stronę równania i uprość wynik. |
|
x = 2 ± 1 |
|
Punkty przecięcia to: x = 2 −1 = 1 i x = 2 + 1 = 3.
Łatwo zauważyć, że zapisanie funkcji w postaci f(x) = (x − 2)2 − 1 daje nam dużo informacji. Mówi nam, jak wykres jest przesunięty w pionie i poziomie. Pokazuje nam również, gdzie znajduje się oś symetrii, a także możemy łatwo znaleźć punkty przecięcia z osiami x i y.
Ogólna postać równania tak zapisanego to:
f(x) = a(x + r)2 + s
Jak już widzieliśmy a jest współczynnikiem x2.
Oś symetrii opisuje równanie x=-r (lub możemy powiedzieć, że ma taką samą wartość jak r ale z przeciwnym znakiem).
Z tych powodów ważne jest, aby wiedzieć jak zapisać równanie
f(x) = ax2 + bx + c w takiej postaci f(x) = a(x + r)2 + s
Przykład
nr 6
Teraz przyjrzyjmy się, jak możemy zmienić postać funkcji drugiego stopnia, czyli zapisać f(x) = x2 − 4x + 3 w postaci f(x) = (x − 2)2 − 1. Porównując z ogólną postacią:
f(x) = ax2 + bx + c
f(x) = x2 − 4x + 3
Tutaj a = 1
i b = −4
i c = 3 (zatem wykres przecina oś y w 3).
Przyjrzyj się wzorowi skróconego mnożenia (x ± q)2 = x2 ± 2qx + q2.
Widzimy, że współczynnik przy x wynosi 2q,
czyli połowa równa jest q, które jest podnoszone do kwadratu przy
stosowaniu reguły.
W naszym przypadku w wielomianie f(x) = x2 − 4x + 3 ostatni czynnik
musiałby być równy 22
lub 4, jeśli chcielibyśmy wykorzystać regułę do
zapisania wielomianu w postaci nawiasu podniesionego do drugiej
potęgi. Możemy dodać 4 do zadania, a potem je odjąć,
jeśli mamy taką ochotę. Możemy dodać
jakiekolwiek q2,
jeśli je potem odejmiemy. Spróbujmy w ten sposób:
|
f(x) = x2 − 4x + 3 |
Połowa współczynnika przy x to -4/2 = -2 , które podnosimy do kwadratu (4) i dodajemy do równania. |
|
= (x2 − 4x + 22) − 22 + 3 |
|
|
= (x − 2)2 − 4 + 3 |
Nie możemy dodać 22 do równania bez dokonania pewnych poprawek. Musimy również odjąć 4, tak aby równanie pozostało prawdziwe. Teraz upraszczamy -4+3=-1. |
|
= (x − 2)2 − 1 |
Z przykładu powyżej możemy wyciągnąć wniosek, że wykres wielomianu drugiego stopnia (f(x) = x2 + bx + c) ma oś symetrii x = −b/2 (a = 1) i przecina oś y gdy y = c.
Przykład
nr 7
Znajdź oś symetrii wykresu funkcji f(x) = 2x2 − 12x + 10.
W tym przypadku a = 2 zatem reguła z poprzedniego przykładu tutaj się nie stosuje. Nie można więc w prosty sposób przepisać tego równania do takiej postaci. Za to przesuniemy tę funkcję o 10 jednostek w dół przez odjęcie 10 od równania. Przesunięcie wykresu w pionie nie zmienia położenia osi symetrii.
Nazwiemy tę nową funkcję g(x) i znajdziemy gdzie g(x) przecina oś x.
2x2 − 12x = 0
2x(x − 6) = 0
To równanie ma rozwiązanie x = 0 lub 6. Wykres przecina oś x w 0 i 6, zatem oś symetrii musi być w połowie odległości między tymi dwoma punktami, czyli x = 3.
Przykład
nr 8
Zapisz funkcję f(x) = 2x2 − 12x + 10 w
postaci f(x) = a(x + r)2 + s .
|
f(x) = 2x2 − 12x + 10 |
Wyciągnij 2 przed nawias. Połowa współczynnika przy x to 3, zatem dodaj 32 wewnątrz nawiasu. W rzeczywistości dodaliśmy 18, zatem musimy teraz odjąć 2∙32 poza nawiasem. |
|
= 2(x2 − 6x + 32) − 2∙32+ 10 |
|
|
= 2(x2 − 6x + 9) − 18 + 10 |
|
|
= 2(x − 3)2 − 8 |
Teraz widzimy, tak jak poprzednio, że oś symetrii jest w x = 3.
Współczynniki przy
x w przykładzie powyżej (f(x) = 2x2 − 12x + 10) to a = 2, b = −12
i c = 10. W celu znalezienia osi symetrii wyciągamy czynnik 2 przed nawias,
co równoznaczne jest podzieleniu przez a = 2. Potem
dzielimy współczynnik stojący przy x (6) przez 2 i zmieniamy znak liczby.
Ogólny wzór opisujący położenie osi symetrii funkcji f(x) = ax2 + bx + c wygląda więc następująco:
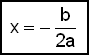
Przykład
nr 9
Znajdź wierzchołek paraboli f(x) = 2x2 − 12x + 10.
Wierzchołek paraboli znajduje się na osi symetrii czyli w x = 3. Wartość y to f(3) = 2∙32 − 12∙3 + 10 = 18 − 36 + 10 = −8.
Wierzchołek znajduje się w punkcie (3, −8).
Zauważ, że jeżeli a>0 to wierzchołek znajduje się w minimalnej wartości funkcji a jeśli a<0 to wierzchołek jest w maksymalnej wartości funkcji.
Przećwicz powyższe przykłady,
a potem zrób test nr 3.
PS Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.