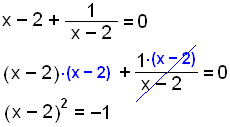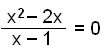|
© 2009 Rasmus ehf og Jóhann Ķsak Pétursson |
Funkcje I |
Prezentacja nr 4
Funkcje wymierne
Funkcje wymierne mają następującą postać:
![]() lub
lub
![]()
Gdzie f(x)
i g(x) są wielomianami i mianownik g(x) ma stopień co najmniej
pierwszy (zawiera czynnik z x).
Teraz przyjrzymy się kilku przykładom funkcji wymiernych i ich
wykresom.
Przykład
nr 1
Najpierw przyjrzyj się funkcji:
![]()
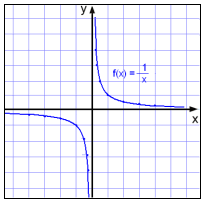
Jeśli zaczniemy robić tabelę wartości, to zauważymy, że x nie może przyjąć wartości 0, co oznaczałoby dzielenie przez 0. Gdy x zbliża się do 0 ale jest dodatni to widzimy, że wartości funkcji (wartości y) stają się coraz większe. Gdy x zbliża się do 0 ale jest ujemny, to wartości funkcji przyjmują coraz większe liczby ujemne.
Wykres tej funkcji wygląda jakby był prawie równoległy do osi y w pobliżu gdzie x=0. Gdy coś takiego się dzieje to mówi się, że wykres ma asymptotę pionową i opisany jest równaniem x = 0.
Przykład
nr 2
Teraz zbadamy funkcję
![]()
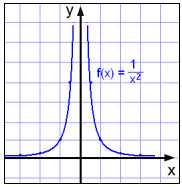
Widzimy, że wartości funkcji stają się coraz większe gdy x zmierza do 0 od prawej (x > 0) i lewej (x < 0) strony.
Znów oś y jest asymptotą pionową.
Również zauważamy, że wykres nigdy nie przecina osi x ani osi y.
Możemy spróbować obliczyć punkty przecięcia i zobaczyć co się stanie.
Znajdujemy miejsce przecięcia wykresu z osią y poprzez obliczenie f(0), jako że współrzędne x wszystkich punktów na osi y równe są 0.
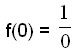
Aby to obliczyć musielibyśmy podzielić przez 0, co jest niemożliwe.
Aby znaleźć miejsca przecięcia osi x musimy
rozwiązać równanie f(x) = 0 lub y = 0, ponieważ wszystkie punkty
na osi x mają współrzędną y równą 0.
|
|
= 0 |
|
1 = 0∙x2 |
|
I znów otrzymujemy równanie, które nie ma rozwiązania. Stąd możemy wyciągnąć wniosek, że wykres nie przecina osi współrzędnych.
Przykład
nr 3
Przyjrzyj się funkcji
![]()
i oblicz gdzie wykres przecina osie współrzędnych.
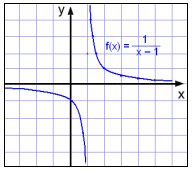

Jeśli x = 1 to będziemy dzielić przez 0 zatem x ≠ 1. Gdy x zbliża się do 1 to wartości y zwiększają się w kierunku liczb dodatnich jeśli x>1 i ujemnych x<1. Tym razem wykres wygląda jakby leżał w pobliżu prostej x = 1.
Aby znaleźć miejsce przecięcia wykresu z osią y obliczamy f(0), ponieważ x = 0 na osi y.
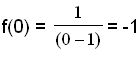
Aby znaleźć miejsce przecięcia osi x rozwiązujemy równanie f(x) = 0 lub y = 0, gdyż wszystkie punkty leżące na osi x mają współrzędną y = 0.
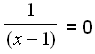
1 = 0∙(x − 1) = 0
Znów otrzymujemy równanie, które nie posiada rozwiązania stąd wniosek, że wykres nie przecina osi x.
Przykład
nr 4
Przyjrzyj się funkcji
![]()
i znajdź wszystkie punkty przecięcia z osiami współrzędnych
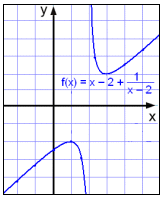
Widzimy, że x ≠ 2 gdyż w przeciwnym razie mielibyśmy 0 w mianowniku. Gdy x zbliża się do 2 z prawej strony, to wartości funkcji stają się coraz większe i wykres idzie do góry. Gdy x zbliża się do 2 z lewej strony, to funkcja osiąga coraz większe wartości ujemne i wykres idzie w dół. Zatem wykres ma pionową asymptotę x = 2.
Wykres przecina oś y gdy x = 0.
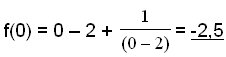
Wykres przecina oś y gdy f(x) =
0. Musimy rozwiązać równanie:
|
|
Kiedy mnożymy przez (x - 2) to otrzymujemy równanie bez rozwiązania. |
Gdy równanie f(x) = 0 nie ma rozwiązania, to wykres nie przecina osi x.
Powyższe przykłady pokazują, że funkcje wymierne prawie zawsze mają pionową asymptotę przechodzącą przez punkt gdzie mianownik jest równy zero.
Funkcja może być obliczona dla wszystkich innych wartości x.
Przykład
nr 5
Na koniec przebadamy funkcję
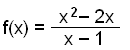
znajdując pionową asymptotę i punkty gdzie wykres przecina osie x oraz y.
Najpierw rozważ dla jakich wartości x nie możemy obliczyć f(x).
Mianownik jest równy 0, czyli:
x − 1 = 0
x = 1
Asymptota pionowa znajduje się w x = 1 a funkcja przyjmuje wartości dla wszystkich x z wyjątkiem x = 1.
{xĪR| x ¹ 1} lub R \ {1}
Następnie znajdź punkt przecięcia osi y przez obliczenie f(0).
f(0) = (0 − 0)/(0 − 1) = 0
Wykres przecina oś y w (0, 0).
Aby znaleźć miejsce przecięcia wykresu z
osią x, musimy rozwiązać równanie f(x) = 0.
|
|
Brot veršur nśll ef teljari žess veršur 0 |
x2 − 2x = 0∙(x − 1) = 0
x(x − 2) = 0
Wykres przecina oś x w x = 0 i x = 2.
Przećwicz powyższe przykłady,
a potem zrób test nr 4.
PS Pamiętaj, żeby
regularnie wypełniać Twoją tabelkę wyników.