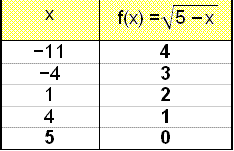|
© 2009 Rasmus ehf og Jóhann Ísak Pétursson |
Funkcje I |
Prezentacja nr 5
Dziedzina i zbiór wartości funkcji
Możemy myśleć o funkcji jak o maszynie lub sekwencji operacji wykonywanych na zbiorze liczb. Liczby wchodzą do maszyny, a inne liczby wychodzą z niej w zależności jak funkcja jest zdefiniowana. Liczby, które możemy włożyć do maszyny nazywane są dziedziną funkcji. Liczby, które wychodzą z niej nazywane są wartościami funkcji.
Liczby (x), które obejmuje
formuła f(x) nazywamy „dziedziną” i oznaczamy Ff. (Jeśli postanowimy
nazywać funkcję g(x) to będzie to dziedzina
Fg). Jeśli dziedzina
nie jest podana to zakładamy, że funkcja jest określona dla
wszystkich liczb w zbiorze liczb rzeczywistych (zbiorze R).
Wyobraźmy sobie teraz, że wszystkie wartości x w dziedzinie zostaną wykorzystane do obliczenia wartości f(x). Taki zbiór nazywany jest zbiorem wartości funkcji lub obrazem i jest oznaczany Vf.
Kiedy ustalamy dziedzinę funkcji musimy brać pod uwagę, że
działania rachunkowe mogą stworzyć nam ograniczenia
dotyczące używanych liczb. Główne
działania ograniczające to dzielenie i pierwiastkowanie.
Musimy wyeliminować z dziedziny liczby, które tworzą dzielenie przez zero albo
pierwiastek z liczby ujemnej.
Trudniej może być znaleźć zbiór wartości
funkcji. Najprostszym sposobem jest obejrzeć wykres i odczytać z
niego granice zbioru wartości funkcji.
Możemy także obliczyć wartości poza granice dziedziny i próbować oszacować, co się dzieje
pomiędzy.
Przykład
nr 1
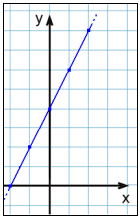
Dana jest funkcja f(x) = 2x + 4. Możemy wybrać jakąkolwiek wartość x, żeby móc obliczyć f(x). Zatem nie musimy ograniczać dziedziny. Wszystkie liczby się nadają, więc Ff = R.
Gdy stworzymy tabelę wartości wybierając
jakiekolwiek wartości x to widzimy, że y przyjmuje wartości
rzeczywiste. Czym większe wybierzemy x tym większa będzie
wartość y. Gdy narysujemy wykres to widzimy,
że jest to prosta, którą możemy przedłużać w obie
strony jak długo tylko chcemy. Zatem zbiorem wartości funkcji jest
również zbiór R.
|
Dziedzina x |
Wartości funkcji f(x) = 2x + 4 |
|
|
-2 |
0 |
|
|
-1 |
2 |
|
|
0 |
4 |
|
|
1 |
6 |
|
|
2 |
8 |
Przykład
nr 2
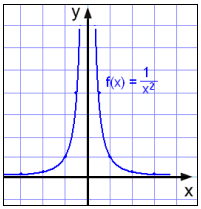
Teraz rozważymy funkcję
![]()
|
Dziedzina x |
Wartości funkcji f(x) = 1/x2 |
|
|
-2 |
1/4 |
|
|
-1 |
1 |
|
|
-1/2 |
4 |
|
|
0 |
Niemożliwe do obliczenia |
|
|
1/2 |
4 |
|
|
1 |
1 |
|
|
2 |
1/4 |
Jedyna wartość, której nie możemy wybrać to x = 0, gdyż musielibyśmy dzielić przez 0. Zatem dziedziną funkcji jest R\{0}.
Widzimy z łatwością jakie otrzymamy wartości y, patrząc na tabelę wartości. Widzimy, jednakże, że f(10) = f(−10) = 1/100 i f(100) = f(−100) = 1/10.000 itd. Gdy x rośnie to y staje się coraz bliższy 0. y nigdy nie przyjmuje wartości 0 i nigdy wartości ujemnych. Gdy x zbliża się do 0, y staje się coraz większe: f(1/10) = f(−1/10) = 100 i f(1/100) = f(−1/100) = 10.000. Podsumowując zbiór wartości funkcji to zbiór liczb rzeczywistych większych od 0: Vf = á0, ®ń.
Przykład
nr 3
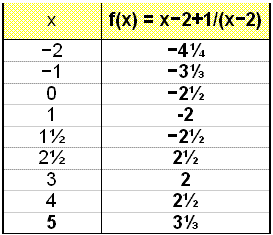
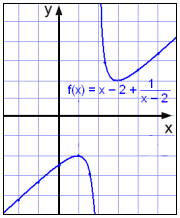
Przyjrzyj się funkcji
![]()
|
Dziedzina: Wartości funkcji: : |
|
Funkcja może być określona dla wszystkich wartości x z wyjątkiem x = 2, stąd dziedziną jest Ff = R\{2}.
Z tabeli wartości oraz z wykresu widzimy, że y przyjmuje wszystkie wartości z wyjątkiem tych z przedziału -2 do 2.
Zbiór wartości funkcji:
Vf = {y Î R│y Ł −2 lub y ł 2}.
Przykład
nr 4
Przyjrzyj się paraboli y = x2 − 2x + 2.

Wiemy, że ramiona paraboli skierowane są do góry gdyż a > 0, zatem wierzchołek jest minimalną wartością. Musimy obliczyć położenie wierzchołka, żeby określić zbiór wartości funkcji. Znajdujemy oś symetrii tak jak poprzednio, korzystając ze wzoru x = −b/2a.
x = −(−2/2) = 1.
Następnie musimy znaleźć wartość y dla x = 1. Zatem obliczamy:
f(1) = 1 − 2×1 + 2 = 1. Wierzchołek jest w punkcie (1, 1) .
Wartości y nigdy nie przyjmują wartości poniżej 1, natomiast przyjmują wartości w nieskończoności.
Zatem zbiór wartości funkcji f(x) to Vf = [1, ®ń.
Przykład
nr 5
Znajdź dziedzinę i zbiór wartości funkcji
![]()
|
Dziedzina: Wartości funkcji:
|
|
Nie możemy określić funkcji dla każdego x powyżej 5, ponieważ oznaczałoby to
obliczenie pierwiastka z liczby ujemnej. Możemy, jednakże,
wybrać jakiekolwiek inne x włącznie z wartościami ujemnymi
x, ponieważ wtedy otrzymamy dwa znaki minus przed x (−− = +) pod pierwiastkiem.
Dziedzina to:
|
|
lub taki |
|
Ff = {xÎR│x Ł 5} = |
Ff = á¬5] |
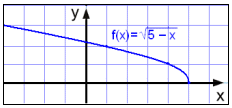
Aby znaleźć zbiór wartości funkcji tworzymy tabelę wartości i przyglądamy się wykresowi.
Widzimy, że wykres kończy się w punkcie (5, 0),
ale możemy go przedłużać w lewo do góry jak długo
tylko chcemy. Wartości y nigdy nie osiągają wartości
poniżej 0. Zatem:
|
Można to zapisać w taki sposób |
lub taki |
|
Vf = {yÎR│y ł 0} = |
Vf = [0, ®ń |
Przypomnienie: Wartości x decydują o dziedzinie, a wartości y decydują o zbiorze wartości.
Przećwicz powyższe przykłady,
a potem zrób test nr 5.
PS Pamiętaj, żeby
regularnie wypełniać Twoją tabelkę wyników.