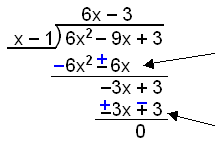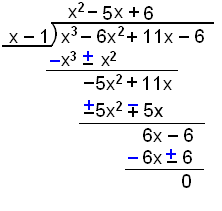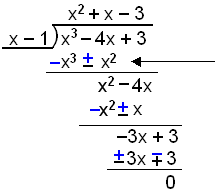© 2009  Rasmus ehf    og Jóhann Ísak Pétursson

Rozkład wielomianu na czynniki


Drukuj

Prezentacja nr 1

Dzielenie wielomianów i twierdzenie Bézouta

Przyjrzyj się wielomianowi f(x) = 6x2 − 9x + 3 i wybierz kilka wartości x do stworzenia tabeli wartości. Wyobraź sobie, że mamy na tyle szczęścia by wybrać x = 1 i zauważyć, że f(1) = 0.

Jeśli x = 1 to (x - 1) = 0. To, że f(1) = 0 mówi nam, że (x - 1) jest czynnikiem f(x). Jeśli założymy, że (x - 1) jest czynnikiem f(x) to możemy również pokazać, że f(1) = 0:

    f(x) = 6x2 − 9x + 3 = (nieznany czynnik)(x - 1)

    f(1) = 6 − 9 + 3 = (nieznany czynnik)(1 − 1) = (nieznany czynnik)∙0

           = 0

Jako że dzielenie jest działaniem odwrotnym do mnożenia, to musimy podzielić wielomian 6x2 − 9x + 3 przez x − 1, aby znaleźć nieznany czynnik. Teraz nauczymy się to robić przez porównanie dzielenia wielomianów do zwykłego dzielenia liczb, którego się nauczyliśmy.

Przykład nr 1

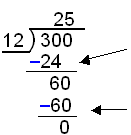
Dzielenie liczb:

Ile razy 12 mieści się w 30?
Odpowiedź to 2. Teraz przemnóż 
2∙12 = 24.
Odejmij 24 od 30 i przenieś 0 w dół.

Ile razy 12 mieści się w 60?
5 razy. 5∙12 = 60.
Odejmij 60 od 60.

Dzielenie wielomianów:

Ile razy x − 1 mieści się w 6x2?
6x razy.  6x∙(x − 1) = 6x2 − 6x. Odejmij 6x2 − 6x przez zmianę znaku przed każdym wyrażeniem. Przenieś w dół +3.

Ile razy  x − 1 mieści się w -3x? 
-3 razy. −3∙(x − 1) = −3x + 3. Odejmij −3x + 3  przez zmianę znaku przed każdym wyrażeniem. Reszta równa jest 0.

f(x) = 6x2 − 9x + 3 można rozłożyć na czynniki (6x − 3)(x − 1).

Przykład nr 2

Możemy rozłożyć na czynniki 6x2 − 9x + 3 stosując wzory na pierwiastki równania kwadratowego.

Współczynniki równania to a = 6, b = −9 i c = 3.

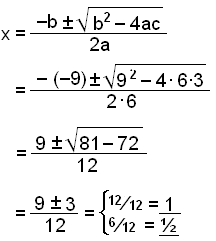
Rozwiązaniami równania są 1 i ˝, zatem (x − 1) i (x − ˝) są czynnikami w równaniu 

6x2 − 9x + 3. Otrzymujemy zatem:

    6x2 − 9x + 3 = 6(x − 1)(x − ˝).

Można to sprawdzić przemnażając przez siebie wyrażenia w nawiasach.

Przykład ten wskazuje nam regułę na rozkładanie na czynniki funkcji kwadratowej:

ax2 + bx + c = a(x − r1)(x − r2)

Współczynniki r1 i r2 nazywane są pierwiastkami równania.

Przykład nr 3

Teraz podzielimy x3 − 6x2 + 11x − 6 przez x − 1, a wynik użyjemy do rozłożenia na czynniki wielomianu.

x mieści się x2 razy w x3.
x2(x − 1) = x3 − x2.
Odejmijmy x3 − x2 przez zmianę znaku przed każdym wyrażeniem.

x mieści się −5x razy w −5x2.
−5x(x − 1) = −5x2 − 5x.
Odejmijmy −5x2 + 5x przez zmianę znaku przed każdym wyrażeniem.

x mieści się 6 razy w 6x.
6(x − 1) = 6x− 6.
Odejmijmy 6x - 6 przez zmianę znaku przed każdym wyrażeniem.

Reszta wynosi 0, co oznacza, że (x - 1) jest czynnikiem wielomianu.

x3 − 6x2 + 11x − 6 = (x2 − 5x + 6)(x − 1) = (x − 3)(x − 2)(x − 1)

Przykład nr 4

Teraz przyjrzyjmy się trudniejszemu przykładowi.

Podziel wielomian x3 − 4x + 3 przez x − 1, a potem rozłóż na czynniki.

W tym przypadku nie możemy odjąć  x2 od −4x. Zatem oba wyrażenia pozostają bez zmian.

Reszta z dzielenia wynosi 0 zatem x - 1 jest czynnikiem wielomianu. Teraz pozostaje rozłożyć na czynniki x2 + x − 3. Musimy użyć do tego celu wzorów na pierwiastki równania kwadratowego.

Współczynniki to a = 1, b = 1 i c = −3.

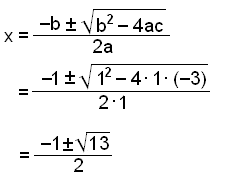
Wielomian rozłożony na czynniki:

x3 − 4x + 3 = (x2 + x − 3)(x − 1)

Przykład nr 5

Teraz przyjrzyjmy się przykładowi, gdzie reszta z dzielenia nie jest równa 0. Podziel x3 + 4x2 + x + 1 przez x + 1.

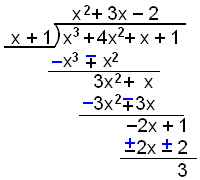
W tym przykładzie reszta jest równa 3.

Możemy teraz przepisać wielomian:

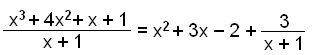
Sposób zapisu wyniku jest ważny.

Z tego przykładu widzimy następujący ogólny wynik:

Jeśli pomnożymy obie strony równania przez x − a to otrzymamy następujący zapis wielomianu f(x):

   f(x) = q(x)(x − a) + reszta

Teraz wykorzystamy tę wersję równania f(x), aby obliczyć f(a).

    f(a) = q(a)(a − a) + reszta

    f(a) = q(x)∙0 + reszta

    f(a) = reszta

To nam pokazuje, że możemy znaleźć resztę, gdy wielomian jest dzielony przez  x – a, bez wykonywania jakiegokolwiek dzielenia.

To twierdzenie jest nazywane twierdzeniem Bézouta i brzmi:

    Jeśli wielomian f(x) jest podzielny przez x − a, to reszta równa jest f(a).

Przykład nr 6

Wykorzystaj twierdzenie Bézouta do znalezienia reszty z dzielenia wielomianu x3 + 4x2 + x + 1 przez  x + 1.

Twierdzenie Bézouta obowiązuje dla dzielenia przez x – a. Jeśli chcemy je użyć dla dzielenia przez x + 1, to musimy obliczyć f(-1).

    f(−1) = (−1)3 + 4∙(−1)2 + (−1) + 1

            = −1 + 4 − 1 + 1

            = 3

To zgadza się z wynikiem w przykładzie 5.

Przykład nr 7

Na koniec użyjemy twierdzenia Bézouta do znalezienia reszty z dzielenia x3 + 4x2 + x + 1 przez x − 1.

Stosujemy twierdzenie Bézouta dla a = 1 i znajdujemy resztę z dzielenia f(x) przez x − 1 obliczając f(1).
 

    f(1) = 13 + 4∙12 + 1 + 1

          = 1 + 4 + 1 + 1

          = 7

Przećwicz powyższe przykłady, a następnie zrób test nr 1.

PS Pamiętaj regularnie wypełniać Twoją tabelkę wyników.