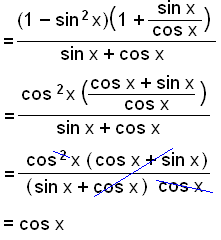|
© 2009 Rasmus ehf og Jóhann Ísak |
Trygonometria |
Prezentacja nr 1
Twierdzenie Pitagorasa w postaci trygonometrycznej
Matematyka posiada wiele
twierdzeń, które pozwalają nam upraszczać problemy i tym samym
rozwiązywać skomplikowane równania trygonometryczne. Teraz spróbujemy
poznać jedno z nich, prawdopodobnie to najbardziej przydatne.
|
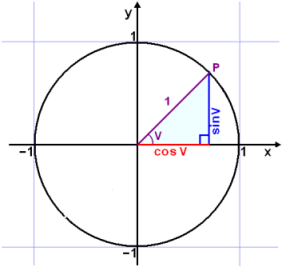
Twierdzenie to często nazywane jest twierdzeniem Pitagorasa w postaci trygonometrycznej lub jedynką trygonometryczną. Twierdzenie Pitagorasa jest prawdziwe dla wszystkich punktów P, które znajdują się na jednostkowym okręgu. To oznacza, że: |
|
|
sin 2 v + cos 2 v = 1 |
To równanie może
być zapisane na dwa sposoby:
|
sin 2 v = 1 − cos 2 v |
i
|
cos 2 v = 1 - sin 2 v |
Przykład nr 1
Znajdź sin
x jeśli cos x = ⅓ i 0 ![]() x < p/2 (x jest
kątem z przedziału 0° do 90°).
x < p/2 (x jest
kątem z przedziału 0° do 90°).
Możemy rozwiązać ten problem używając kalkulatora, cos−1 (⅓) ≈ 70,53° a zatem sin 70,53° ≈ 0,94. Jeśli chcemy dokładne rozwiązanie, to możemy rozwiązać ten przykład bez kalkulatora wykorzystując twierdzenie Pitagorasa w postaci trygonometrycznej.
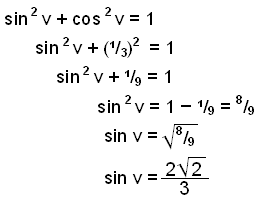
Przykład nr 2
Wykorzystaj związek sin2 v + cos2 v = 1, aby zapisać w inny sposób 1/ cos 2 v.
Jednym ze sposobów jest przeniesienie sin2 v na drugą stronę równania, tak by otrzymać cos2 v = 1 − sin2 v, a następnie odwrócić obie strony równania. Dzięki temu otrzymamy:
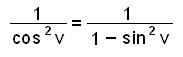
Jest też inny niezbyt oczywisty sposób, który prowadzi do bardzo przydatnej postaci wyrażenia. Zwróć uwagę co się stanie jeśli podzielimy oryginalne równanie sin2 v + cos2 v = 1 przez cos2 v.
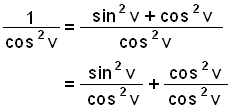
![]()
Teraz udowodniliśmy twierdzenie:
![]()
Przykład nr 3
Teraz użyjemy twierdzenia Pitagorasa w postaci trygonometrycznej do znalezienia wartości sin2 v i cos2 v przy założeniu, że sin2 v = cos2 v.
Najpierw zastępujemy cos2 v przez cos2 v = 1 − sin2 v.
sin2 v = cos2 v
sin2 v = 1 − sin2 v
2∙sin2 v = 1
sin2 v = ˝
Teraz zastępujemy sin2 v przez sin2 v = 1 − cos2 v.
sin2
v
= cos2 v
1 − cos2 v = cos2 v
1 = 2∙cos2
v
cos2
v = ˝
Przykład nr 4
Rozwiąż równanie cos2 x = sin x + 1
cos2 x = sin x + 1
1 − sin2 x = sin x
+ 1
0 = sin2 x + sin x = sin
x (sin x + 1)
To prowadzi do sin x = 0 albo sin x = −1.
zatem x = k∙p (k∙180°) lub x = 3p/2 + k∙2p (270° + k∙360°).
Przykład nr 5
Uprość
wyrażenie
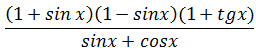
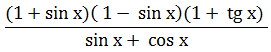
|
|
Tutaj używamy wzoru skróconego mnożenia (a + b)(a − b) = a2 − b2 a potem zapisujemy tg jako sin/cos i upraszczamy
|
Przećwicz
powyższe przykłady, a potem zrób test nr 1.
PS Pamiętaj, aby regularnie wypełniać Twoją tabelkę wyników.