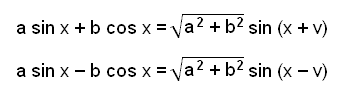|
© 2009 Rasmus ehf og Jóhann Ķsak |
Trygonometria |
Prezentacja nr 3
Równania typu a sin x + b cos x = c
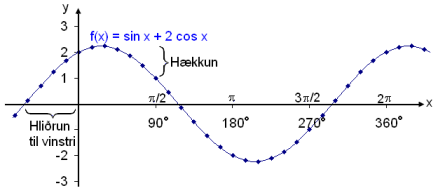
Rysunek przedstawia wykres f(x) = sin x + 2 cos x.
Hlišrun til vinstri = Przesunięcie w
lewo, Hękkun =
Przyrost
GAT EKKI BREYTT ŽESSARI MYND..
O dziwo wykres wygląda jak zwykła sinusoida, która została przesunięta w bok i jej amplituda zwiększona w porównaniu do podstawowej fali. Widzieliśmy wcześniej, co wpływa na amplitudę i jak amplituda może zostać zwiększona przez pomnożenie przez stałą większą od 1 (patrz prezentacja Funkcje Trygonometryczne 3). Widzieliśmy również, że wykres podstawowej funkcji może zostać przesunięty wzdłuż osi x poprzez dodanie stałej do kąta. Wiedząc to wszystko możemy przepisać równanie w postaci:
m sin (x + v) = sin x + 2 cos x
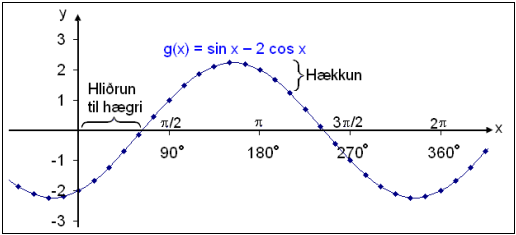
Teraz przyjrzyj się wykresowi g(x) = sin x − 2 cos x.
Hlišrun til haegri = Przesunięcie w
prawo, Hękkun =
Przyrost
LAGA MYND
To jest oczywiście ta sama krzywa z wyjątkiem tego, że przesunięcie jest w drugą stronę niż poprzednio. Teraz krzywa przesunięta jest w prawo o tą samą wartość, co początkowa krzywa była przesunięta w lewo. Teraz możemy stworzyć poprawne równanie:
m sin (x − v) = sin x − 2 cos x
Teraz przepisujemy wyrażenie stosując wzory na sinus różnicy i sinus sumy kątów:
sin (x + v) = sin x cos v + cos x sin v
sin (x − v) = sin x cos v − cos x sin v
Mnożąc obie strony przez m otrzymujemy:
m sin (x + v) = m sin x cos v + m cos x sin v
m sin (x − v) = m sin x cos v − m cos x sin v
Porównaj wynik z początkowymi równaniami:
m sin (x + v) = 1 sin x + 2 cos x
= m cos v sin x + m sin v cos x
m sin (x − v) = 1 sin x − 2 cos x
= m cos v sin x − m sin v cos x
Widzimy, że w obu przypadkach muszą być spełnione:
m cos v = 1
m sin v = 2
Jeśli podzielimy dolne
równanie przez górne to otrzymamy:
tg v = 2/1
Co da nam kąt v = tan−1 (2) ≈ 63,4°.
Jeśli narysujemy trójkąt prostokątny o krótszych bokach długości 1 i 2, czyli wartościach takich jak w równaniu, to będziemy mogli obliczyć długość przeciwprostokątnej.
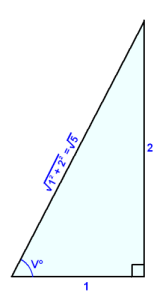
Widzimy, że:
cos
v = 1/
i sin v = 2/.
Wykorzystując równania:
m cos v = 1
m sin v = 2.
Otrzymujemy:
m∙1/ = 1
m =
Inaczej możemy zapisać równania:
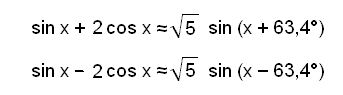
Widzimy, że amplituda
fali w równaniu f(x) = sin x + 2 cos x i g(x) = sin x − 2 cos x to .
Uogólniając i
używając a i b jako stałe otrzymujemy poniższą
zasadę:
|
|
Kąt v może
być znaleziony z:
|
tg v = b/a gdzie a > 0, b > 0 i 0° < v° < 90° |
Przykład nr 1
Znajdź amplitudę funkcji f(x) = 3 sin x + 4 cos x.
Zaczynamy od przepisania funkcji w postaci:
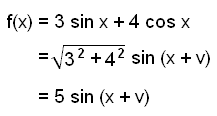
Amplituda równa jest 5.
Przykład nr 2
Wykres funkcji f(x) = 3 sin x + 4 cos x to przesunięta sinusoida.
Oblicz o ile stopni i w którą stronę fala została przesunięta.
f(x) = 3 sin x + 4 cos x
= 5 sin (x + v)
v = tg −1 (4/3) ≈ 53,1°
Fala została przesunięta o 53,1° w lewo (f(x) ≈ 5 sin (x + 53,1°).
Przykład nr 3
Dana jest funkcja f(x) = 5 sin x + 12 cos x + 3. Znajdź amplitudę, maksymalną wartość oraz przesunięcie fali.
Przepisujemy f(x).
tg −1 (12/5) ≈ 67,4°
f(x) = 13 sin (x + 67,4°) + 3
Amplituda wynosi 13, zatem wartość maksymalna to 13 + 3 = 16 . Przyjrzyjmy się wykresowi.
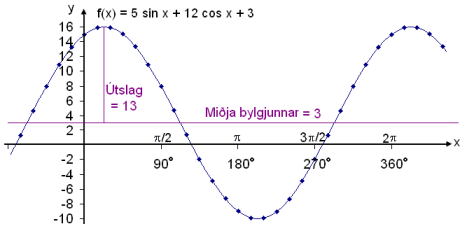Utslag =
Amplituda, Midja bylgjunnar
= środek fali
LAGA MYND
Przykład nr 4
Rozwiąż równanie
3 sin x + 4 cos x = 5 w przedziale 0° 
x < 360°.
3 sin x + 4 cos x = 5
= 5 sin (x + 53,1°)
sin (x + 53,1°) = 5/5 = 1
x + 53,1° = sin −1 1 = 90° + k∙360°
x = −53,1° + 90° + k∙360°
x = 36,9°
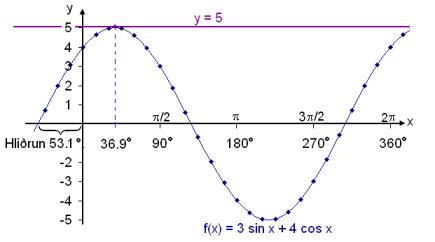
Otrzymujemy jedno rozwiązanie 36,9° w pierwszej ćwiartce.
Widzimy, że na wykresie nie ma innego rozwiązania w podanym przedziale.
Przykład nr 5
Znajdź
rozwiązanie równania sin x − 
cos x = 1.
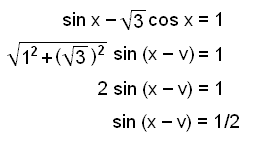
Widzimy,
że tg v = i v = tg () −1
= p/3 (60°).
sin (x − p/3) = ½
|
(x − p/3) = sin −1 (½) = p/6 + k∙2p |
p/6 = 30° |
x = p/3 + p/6 + k∙2p
= p/2 + k∙2p
lub
(x − p/3) = p − p/6 + k∙2p
x = p/3 + p − p/6 + k∙2p
|
x = 7p/6 + k∙2p |
7p/6 = 210° |
Przećwicz
powyższe przykłady, a potem zrób test nr 3.
PS Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.