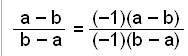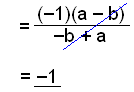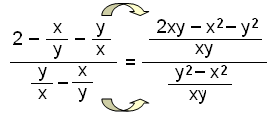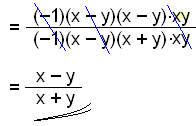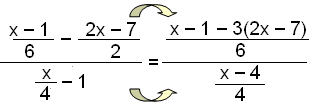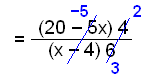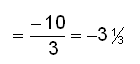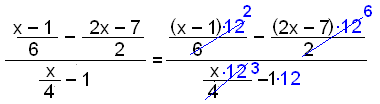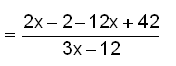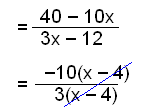|
© 2009 Rasmus ehf og Jóhann Ísak Pétursson |
Ułamki ułamków |
Prezentacja nr 2
Przyjrzyjmy się bardziej skomplikowanym przykładom.
Przykład nr 1
|
|
|
|
|
Możemy przemnożyć licznik i mianownik przez -1 bez zmieniania ułamka. |
|
|
Jeśli przemnożymy wyrażenie w mianowniku przez -1, to otrzymamy to samo wyrażenie, co w nawiasie w liczniku. Zostawiamy w liczniku -1 poza nawiasem i skracamy. |
Możemy podsumować rezultat powyższego przykładu prostą regułą:
Ta reguła stosuje się do ułamków, w których licznik i mianownik są takie same z wyjątkiem tego, że wszystkie wyrazy w liczniku mają przeciwny znak do wyrazów w mianowniku.
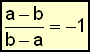
Przykład nr 2
|
|
|
|
|
Dodajemy do siebie wyrazy w liczniku znajdując wspólny mianownik. Robimy to samo z mianownikiem. |
|
|
Teraz możemy zamienić dzielenie w mnożenie, tak jak poprzednio, i umieścić dwa ułamki na jednej kresce ułamkowej. Ostatecznie wyłączamy czynniki przed nawias i skracamy. |
Przykład nr 3
|
|
|
|
|
Najpierw dodajemy do siebie wyrazy w liczniku i mianowniku, a następnie umieszczamy dwa ułamki na jednej kresce ułamkowej. |
|
|
Uprość, wyłącz czynnik przed nawias i skróć ułamek. |
|
|
.Zauważ, że −5(x − 4) = 20 − 5x. |
Czasami jest łatwiej przemnożyć licznik i mianownik przez wspólny mianownik wszystkich ułamków.
Przykład nr 4
|
|
|
|
|
Wspólnym mianownikiem wszystkich ułamków w tym przykładzie jest 12. |
|
|
Mnożymy każdy wyraz przez 12, upraszczamy i wyciągamy przed nawias |
|
|
Ostatecznie wyciągamy czynnik przed nawias i upraszczamy jak się da. |
|
|
|
Przećwicz powyższe przykłady, a potem zrób test nr 2.
PS Pamiętaj, żeby
regularnie wypełniać Twoją tabelkę wyników.