© 2000 - 2009   Rasmus ehf

Obliczanie powierzchni

Prezentacja nr 4

   Pole i obwód koła

  

 

O = Długość czarnej linii, która tworzy koło, nazywana jest obwodem. Jego długość oznaczamy O.

d = Średnica to cięciwa, przechodząca przez środek koła i na rysunku jest zaznaczona kolorem niebieskim.

r = Promień to odcinek łączący środek koła z jego brzegiem. Na rysunku jest zaznaczony kolorem  czerwonym.

Jeśli zmierzysz obwód i średnicę i podzielisz je przez siebie to otrzymasz liczbę Pi, która wynosi 3,14.

Liczba Pi jest często zapisywana grecką literką .

Antyczni Grecy używali tego znaku  do oznaczania proporcji między obwodem i średnicą koła. Jeśli nie masz znaku na kalkulatorze to możesz używać ogólnie przyjętego przybliżenia, czyli liczby 3,14. Jest ona wystarczająco dokładna do większości obliczeń.

 

Kilka wzorów, które dobrze jest znać i jeszcze lepiej rozumieć.

Symbol	Nazwa	Wzór
	Pi	= O/d
d	Średnica	d = 2 ∙ r    i   d =  O/
O	Obwód	d ∙ = O
r	Promień	r = d/2
S	Pole powierzchni	S = r2 ∙

 

Kilka przykładów

Przykład nr 1

 

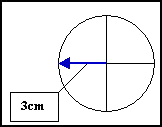
Obliczmy średnicę.     d = 2 ∙ 3cm = 6cm 

Przykład nr 2

Obliczmy obwód.     O = d ∙ = 6cm ∙ = 18,8cm 

Przykład nr 3

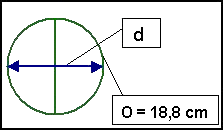
Obliczmy średnicę.     d = ^O/ = ^18,8cm /   = 6 cm   

Przykład nr 4

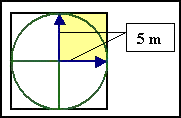
    Pole powierzchni wynosi:     S = r² ∙

S = 5m∙ 5m ∙   78,5 m²

   (Uwaga! Znak  oznacza „w przybliżeniu”.)

Znasz wzór na pole prostokąta. Mały żółty prostokąt jest jedną czwartą dużego.

Mały prostokąt ma pole S = 5m ∙ 5m = 25m², więc cały duży prostokąt ma pole S = 4∙ 25m² = 100m².

Widzimy, że koło ma mniejszą powierzchnię niż duży prostokąt, bo jest w niego wpisane. Znając powierzchnię małego kwadratu możemy ją pomnożyć przez liczbę Pi i otrzymamy pole powierzchni koła, czyli S = ∙ 25m² = 78,5m².

Przećwicz powyższe przykłady, a potem zrób test nr 4.

PS Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.