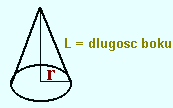© 2000 - 2009 Rasmus ehf |
Obliczanie powierzchni |
Prezentacja nr 5
Jednostki miary powierzchni oraz pole powierzchni brył
Jednostki miary powierzchni:
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
1 |
00 |
00 |
1 m2 = 100 dm2 = 10.000 cm2 |
|
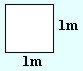
S = 1m ∙ 1m = 1m2 |
|
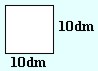
S = 10dm ∙ 10dm = 100dm2 |
|
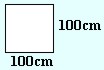
S = 100cm ∙ 100cm = 10.000cm2 |
Obliczyłeś pole pewnego obszaru, np:
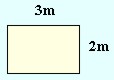
S = 3m ∙ 2m = 6m2 sześć metrów kwadratowych.
A jeśli chcesz zapisać wynik w centymetrach kwadratowych, możesz skorzystać z tabelki miar:
km2 |
hm2 |
dam2 |
m2 |
dm2 |
cm2 |
mm2 |
6 |
00 |
00 |
6 m2 = 60.000 cm2 |
Inny dobry sposób na rozwiązywanie takich zadań to zamiana na centymetry na samym początku.
 =
= 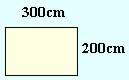
S = 300cm ∙ 200cm = 60.000 cm2
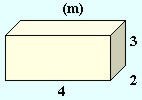
Pole powierzchni prostopadłościanu. Musisz obliczyć powierzchnię wszystkich ścian.
|
|
3m · 4m = 12m2 |
|
2m · 3m = 6m2 |
|
|
2m · 4m = 8m2 |
12m2 + 6m2 + 8m2 = 26m2
Lecz to były tylko trzy ściany. Prostopadłościan ma trzy kolejne ściany identyczne z tymi. Pole powierzchni wynosi więc:
2
· 26m2
= 52m2
Żeby obliczyć pole powierzchni bryły trzeba wpierw rozpoznać figury, z których składają się ściany.
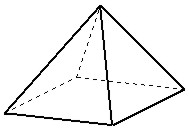
|
Pole powierzchni piramidy = |
Pole powierzchni prostokąta + pole powierzchni czterech trójkątów. |
|
Pole powierzchni piramidy = |
|
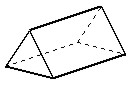
|
Pole powierzchni graniastosłupa |
|
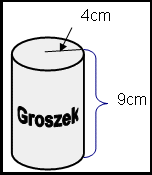
| Pole powierzchni puszki = | wieczko |
dno |
powierzchnia boczna puszki | |||
 |
+ |
 |
+ |
|
|
Powierzchnia wieczka |
S = r2
·
|
|
Powierzchnia dna |
Jest taka sama jak wieczka. |
Rozwinięty bok jest prostokątem:
|
9 cm |
S = długość · szerokość = 9cm · 25,12cm = 226,08cm2 |
|
25,12 cm |
||
|
Ten bok jest obwodem koła. O = d ·
|
||
|
Pole powierzchni puszki = |
|
|
S = |
|
|
Pole powierzchni bocznej stożka = |
|
 |
Pole powierzchni kuli = |
|
Przećwicz powyższe przykłady, a potem zrób test nr 5.
PS Pamiętaj, żeby regularnie wypełniać Twoją tabelkę wyników.