Rasmus.is - Rozkładanie na czynniki

Rozkładanie na czynniki

Prezentacja nr 2

Przypomnijmy sobie zasady mnożenia przez siebie nawiasów.

Każdy wyraz w pierwszym nawiasie mnoży się przez każdy wyraz w drugim nawiasie.

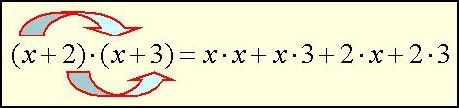
Potem wykonujemy obliczenia i otrzymujemy wynik:

Jeśli mamy rozłożyć na czynniki wyrażenie z trzema członami, które nie mają wspólnego czynnika, to jedyna możliwość to stworzyć iloczyn dwóch nawiasów.

Zobacz wzory skróconego mnożenia:

Wzór skróconego mnożenia – kwadrat sumy:

Wzór skróconego mnożenia – kwadrat różnicy:

Wzory te są po raz pierwszy wprowadzone w materiałach dla klasy 9, lecz będą szerzej omawiane w 10 klasie oraz w szkole średniej.

Kilka przykładów:

x² + 7x + 10 = (x + 2)(x + 5)

x²- 3x - 10 = (x + 2)(x - 5)

x²-9 = (x +3)(x - 3)
Wzór skróconego mnożenia - różnica kwadratów:

x²+ 6x + 9 = (x + 3)(x + 3)
Wzór skróconego mnożenia – kwadrat sumy:

x²- 6x + 9 = (x - 3)(x - 3)
Wzór skróconego mnożenia – kwadrat różnicy:

Teraz zrób test nr 2.

x² + 7x + 10 = (x + 2)(x + 5)
x²- 3x - 10 = (x + 2)(x - 5)
x²-9 = (x +3)(x - 3)	Wzór skróconego mnożenia - różnica kwadratów:
x²+ 6x + 9 = (x + 3)(x + 3)	Wzór skróconego mnożenia – kwadrat sumy:
x²- 6x + 9 = (x - 3)(x - 3)	Wzór skróconego mnożenia – kwadrat różnicy: