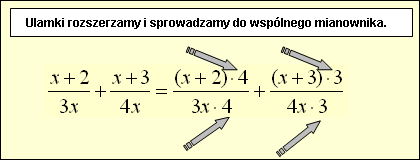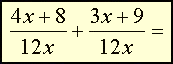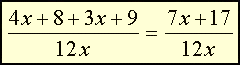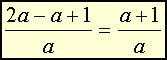© 2000 - 2009   Rasmus ehf

Ułamki zwykłe – dodawanie i odejmowanie

 

Prezentacja nr 3

1. Najpierw sprawdź, czy ułamki mają wspólny mianownik.

3x · 4 = 12x   i   4x · 3  = 12x

Ułamki rozszerzamy i sprowadzamy do wspólnego mianownika.


Poźniej mnożymy i obliczamy nawiasy znajdujące się nad kreską ułamkową.

Wtedy widzimy, że (x + 2)·4 = 4x + 8  i (x + 3)·3 = 3x + 9

  


Otrzymujemy wspólny mianownik, czyli 12x.
     

 

Następnie dodajemy do siebie wyrazy podobne i skracamy.

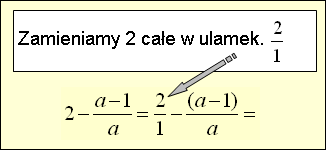
2. Czasami musimy zapisać liczby w nieco innej postaci.

 

 

  

Usuwamy nawias, pamiętając o zmianie znaku przy wyrazach wewnątrz nawiasu.
-(a - 1)  będzie -+a lub - a i - -1 będzie +1.  

Następnie porządkujemy wyrazy podobne i zapisujemy odpowiedź.

3. Bardziej skomplikowane zadania.

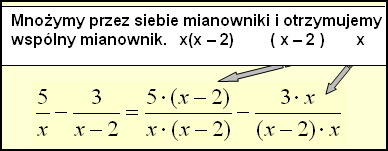
Mnożymy przez siebie mianowniki i otrzymujemy wspólny mianownik.

 

  

Takie równanie jest poddane pewnym ograniczeniom, ponieważ mianownik nie może nigdy równać się 0. x(x - 2) będzie = 0 jeśli x = 2 lub x = 0. Wtedy mówimy, że x nie może przyjmować wartości 0 i +2.

4. Mnożenie dwóch nawiasów.

Mnożymy mianowniki i otrzymujemy wspólny mianownik.

 

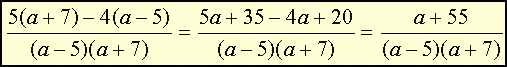
Włączamy czynnik do wnętrza nawiasu, usuwamy nawiasy i porządkujemy wyrazy podobne.

Teraz spróbuj wykonać test nr 3. Jeśli osiągniesz ponad 80% poprawnych odpowiedzi, spójrz w lustro i powiedz: “Jestem mistrzem algebry!”.